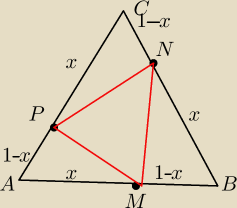
Trojkat rownoboczny 6latek: Dany jest trojkat rownoboczny ABC .Na bokach trojata AB BC i CA zaznacz odpowiednio punkty M, N, P tak ze AM= BN=CP =x i AB=1dm . Zbadaj pole trojkta MNP jako funkcje x

	a2√3
Ogolnie to Ptr=
	4

	√3
Pole duzego trojkata P=		[dm2]
	4

	(1−x)2√3
P(MNP)=
	4

Nie bardzo wiem co dalej z tym zrobic

6latek: Teraz patrze .jest cos nie tak Bede starl sie to rozwiazac jak wroce do domu

ite: 1/ uzasadnij, że czerwony trójkąt jest równoboczny 2/ oblicz długość boku czerwonego trójkąta, np. z tw.cosinusów

===: ... albo od pola podstawowego trójkata odejmij pola trzech trójkącików (wyliczone w funkcji od x)

6latek: dziekuje za uwagi ja to zrobie pozniej Wydaje mi sie ze dla obliczenia pola trojkata np MBN moge skorzystac z ewzoru P=0,5*x*(1−x)*sin60^o

6latek:

	√3
sin60o)=
	2

pole malego trojkata

	1		√3		√3x(1−x)
Pm=		*		(x(1−x)=
	2		2		4

	√3		3√3x(1−x)
P(MNP)=		−
	4		4

	√3−3√3x+3√3x2
P(MNP)=
	4

	√3(1−3x+3x2
P(MNP)=
	4

zapisane jako funkcja

	√3(1−3x+3x2
f(x)=
	4

===================== Powinno byc dobrze

6latek: Natomiast to co proponuje ite

	1
MP2= x2+(1−x)2−		*2*x(1−x)
	2

MP²= x²+1−2x+x²−(x−x²) MP²= 3x²−3x+1 p(MNP)= (3x²−3x+1)√3}{4} Wyszlo to samo Uzasadnienie dlaczego to trojkat MNP jest rownoboczny (to nie za bardzo wiem jak to uzasadnic) Tutaj bym prosil o odpowiedz . pewnie bedzie prosta

ite: trójkąty ΔAPM, ΔBNM i ΔCNP są przystające (bkb) → wszystkie boki mają odpowiednio równe

6latek: Nie pomyslaem o tym dziekuje Ci