zadanko maturalne,pomocy Matura2020: W ostrosłupie prawidłowym trójkątnym kąt między dwiema sąsiednimi ścianami bocznymi ma miarę 2α. Przez krawędź podstawy poprowadzono płaszczyznę prostopadłą do przeciwległej krawędzi bocznej ostrosłupa. Wykaż, że tworzy ona z płaszczyzną podstawy taki kąt β, że √3 *tgα * cosβ=1.

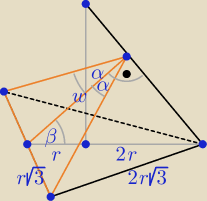
Bogdan: r − długość promienia okręgu wpisanego w podstawę ostrosłupa, podstawą jest trójkąt równoboczny.

	w
cosβ =		⇒ w = 3r*cosβ
	3r

	r√3
tgα =		⇒ r√3 = w*tgα ⇒ r√3 = 3r*cosβ * tgα ⇒ 1 = √3*cosβ*tgα
	w

Eta:

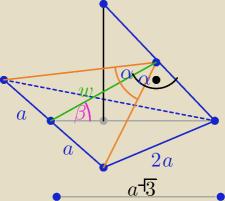
	w		a
cosβ=		⇒w=a√3*cosβ i tgα=		⇒ a=w*tgα
	a√3		w

to: a=a√3cosβ*tgα ⇒ √3cosβ*tgα=1 ♥♥♥♥♥♥♥♥♥♥

Eta: Sorry nie widziałam wpisu Bogdana

Bogdan: Witaj Eto, to chyba telepatia, bo nasze rysunki i rozwiązania są prawie identyczne. Pozdrawiam

Eta: Witaj Bogdanie Często tak mamy