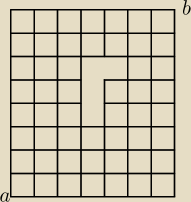
Ile jest najkrótszych dróg z A do B? Nie można przechodzić przez pusty obszar. DandeZ: Ile jest najkrótszych dróg z a do b? Nie można przechodzić przez pusty obszar.

PW: Określ łaskawie na czym polega "droga" − można wykonywać tylko ruchy w poziomie lub pionie, czy na ukos też?

DandeZ: Jakby nie było tego pustego obszaru, to by to wyglądało następująco: w poziomie do przejścia 7 kratek, w pionie 8 czyli razem 15.

	15 7		15 8
A więc najkrótszych dróg z a do b jest		lub		− jest to to samo, a różnica

polega na tym czy wybieramy wszystkie możliwości wyboru w poziomie, czy w pionie.

DandeZ: Idziemy tylko po liniach. W ogóle przepraszam za zamieszanie. Rzeczywiście trochę nie doprecyzowałem.

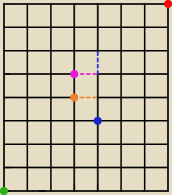
Blee: jeżeli poruszamy się TYLKO w górę albo w prawo i idziemy z zielonego do czerwonego to możemy podejść na dwa sposoby: 1) wyliczyć prawidłowe drogi 2) wyliczyć te drogi które będą szły przez 'niedozwolone' ścieżki Ja wolę tą drugą metodę (mniej kombinowania) Ile jest dróg przez beżową ścieżkę? Dokładnie tyle ile możliwości dotarcia do beżowego punktu i skręcenie w prawo, czyli:

7 4
	*1

fioletowa droga analogicznie:

8 5
	*1

niebieską drogę liczymy trochę inaczej −−− nie chcemy 'zdublować ścieżek' już policzonych wcześniej dlatego bierzemy tylko te ścieżki idące przez niebieską ścieżkę, które dotarły do punktu niebieskiego (a później były 3 ruchy 'do góry' ) więc mamy:

7 3
	*1*1*1

Więc ostatecznie będzie to:

15 8		7 3		7 4		8 5
	−		−		−

Blee: oczywiście źle napisałem, to będzie (odpowiednio)

7 4		7 4
	*1 *

8 5		6 3
	*1 *

7 3		5 2
	*1*1*1 *

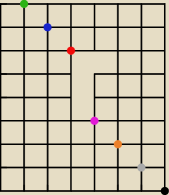
Blee: a jakbyś chciał liczyć 'te dobre' ścieżki to musiałbyś liczyć (np.) w taki sposób: 1) docierasz do punktu zielonego, a później do mety, 2) docierasz do punktu niebieskiego, a później do mety, 3) docierasz do punktu czerownego, a później do mety, 4) docierasz do punktu fioletowego, a później w trzech ruchach masz minimum minimum jeden w prawo, a później do mety, 5) docierasz do punktu beżowego, a później do mety, 6) docierasz do punktu szarego, a później do mety, 7) docierasz do punktu czarnego, a później do mety. Jak widzisz ... wszystko poza punktem (4) bardzo łatwo wypisać, a dla rozrywki możesz się zastanowić nad punktem czwartym (nie licząc z przeciwnego oczywiście )

DandeZ: Dziękuję bardzo