kombinatoryka
student_: Ile jest możliwych rozwiązań równania a+b+c+d=100 gdzie liczby a,b,c,d są naturalne
dodatnie odp N=176851
12 paź 17:40
Saizou :
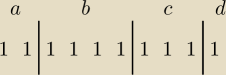
wyobraź sobie ciąg jedynek o długości 100
Teraz chcesz postawiać między te jedynki trzy patyczki (trzy ponieważ chcesz wydzielić
4 sekcje jedynek). Miejsc na te kreski jest 99 a wybieramy tylko 3, zatem mamy
12 paź 17:51
Mila:
Dla a,b,c,d całkowitych nieujemnych mamy:
Dla a,b,c,d całkowitych dodatnich jest tak , jak napisał
Saizou
12 paź 18:09
student_: Bardzo dziękuję za pomoc
13 paź 07:35
student_: Wyjaśnienie tego co napisała Mila bedzie podobne do tego co napisał Saizou.
Dochodzą jeszcze zera których może być co najwyżej 3
13 paź 09:31
Pytający:
"Dochodzą jeszcze zera których może być co najwyżej 3"
Jak już dokładać zera, to musi ich być dokładnie 3.

13 paź 10:13
ite:
Czy zapis 'Dochodzą jeszcze zera' oznacza puste komórki w podziale Saizou czyli
rozszerzenie wartości a,b,c,d na liczby nieujemne?
Dlaczego mają być trzy a nie np. dwie a+b+0+0=100 ?
13 paź 10:42
Pytający:
Cóż,
Student odniósł się do wyjaśnienia
Saizou, więc uznałem, że ma na myśli ciąg 103
elementowy stu jedynek i właśnie dokładnie trzech zer, wtedy różne takie ciągi (których jest
| | | |
| ) odpowiadają różnym rozwiązaniom: |
| | |
(a jedynek) zero (b jedynek) zero (c jedynek) zero (d jedynek)
Natomiast jeśli chodzi o to, ile zmiennych spośród a, b, c, d przyjmuje wartość 0 w możliwym
rozwiązaniu, to oczywiście co najwyżej 3 i może
Student właśnie to miał na myśli, nie
wiem.

13 paź 11:30
ite: Dziękuję za wyjaśnienie.
13 paź 12:23
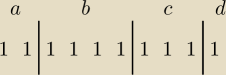 wyobraź sobie ciąg jedynek o długości 100
Teraz chcesz postawiać między te jedynki trzy patyczki (trzy ponieważ chcesz wydzielić
4 sekcje jedynek). Miejsc na te kreski jest 99 a wybieramy tylko 3, zatem mamy
wyobraź sobie ciąg jedynek o długości 100
Teraz chcesz postawiać między te jedynki trzy patyczki (trzy ponieważ chcesz wydzielić
4 sekcje jedynek). Miejsc na te kreski jest 99 a wybieramy tylko 3, zatem mamy

