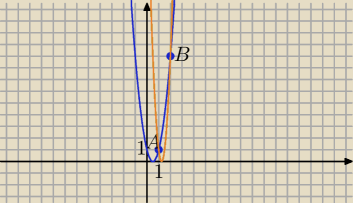
funkcja kwadratowa Master Xie Yi : Znajdz wzor funkcji kwadratowej ktorej wykres jest styczny do osi OX i do ktorego naleza punkty A=(1,1) i B=(2,9) y=ax²+bx+c i c≠0 a+b+c=1 4a+2b+c=9 i delta =0 czyli b²−4*a*0 odejmuje 2 od pierwszego i dostaje 3a+b=8 to b=8−3a z 1 rownania c=1−a−b c=1−a−(8−3a) c= 2a−7 wstawiam do drugiego rownania 4a+2(8−3a)+2a−7=9 4a+16−6a+2a−7=9 0=0 Co jest nie tak

ICSP: Operujesz tylko na dwóch równaniach. Nic nowego z nich nie dostaniesz. Twoją funkcję można zapisać w postaci : y = a(x − b)²

Saizou : a+b+c=1 4a+2b+c=9 b²−4ac=0 a+b+c−(4a+2b+c)=1−9 −3a−b=−8 b=8−3a c=1−a−b c=1−a−(8−3a) c=2a−7 (8−3a)²−4a(2a−7)=0 64−48a+9a²−8a²+28a=0 a²−20a+64=0 Δ=(−20)²−4*1*64=400−256=144

	20−12		8		20+12		32
a1=		=		=4 a2=		=		=16
	2		2		2		2

b₁=8−3*4=8−12=−4 b₂=8−3*16=8−48=−40 c₁=2*4−7=8−7=−1 c₂=3*16−7=48−7=41

Master Xie Yi : dzieki serdeczne

Saizou : poprawka końcówki c₁=−1 c₂=2*16−7=32−7=25 y₁=4x²−4x+1 y₂=16x²−40x+25

Mila: 1) W=(p,0) −wsp. wierzchołka paraboli y=a(x−p)² 9=a*(2−p)² 1=a*(1−p)² stąd:

	1
p=		, a=4
	2

	5
lub p=		, a=16
	4

Master Xie Yi : dzieki Milu

Master Xie Yi : Milu tutaj nie ma y=a(x−p)²+q bo tutaj q=0 bo zbior wartosci tej funkcji to <0,∞)

Mila: W=(p,q)=(p,0) masz napisane w (1)

Master Xie Yi : tak rozumowalem po swojemu

Master Xie Yi : Jeszcze mam pytanie Potrzebne mi sa na razie te rownania funkcyjne ? jesli nie to odstawie bo mam jeszcze ze zbioru 3 zadania z tego do zrobienia .

Master Xie Yi : Wroce do zadania a(2−p)²=9 a(1−p)²=1 4a−4pa+ap²=9 a−2pa+ap²=1 ============= odejmuje 3a−2pa=8 a(3−2p)=8

	8
a=
	3−2p

Wstawiam do drugiego rownania

8
	*(1−p)2=1
3−2p

8(1−p)²= 3−2p

	1
stad mam p=0,5 p=1
	4

Majac p wylicze a Wiec wyszlo mi tak samo jak Tobie

Mila: Ale się namęczyłeś. Ja podzieliłam (1) przez (2) równanie.

(2−p)2
	=9
(1−p)2

4−4p+p²=9*(1−2p+p²) p=... lub p=