wyszlo mi ze ymin = -13 a ymax = -5. czy to jest dobrze czy zle ? S: Oblicz najmniejszą i największą wartość funkcji kwadratowej y=x²−8x+2 w przedziale ⟨3;7⟩

Saizou :

	8
fmin =f(xw)=f(		)=f(4)=42−8*4+2=16−32+2=−14
	3

f_max=f(7)=7²−8*7+2=49−56+2=5

S: dziekuje bardzo

PW: Oj, nie. Jeżeli dobrze napisana dziedzina − otwarty przedział (3, 7) − to f(7) nie jest maksimum. Liczba 7 nie należy do dziedziny.

Saizou : PW ale tam jest przedział obustronnie domknięty

Pan K: PW jest domkniety

PW: Ślepnę, ale wziąłem lupę i widzę dwa "okrągłe nawiasy". Całe życie tak oznaczało się przedział otwarty.

Pan K: Przepraszam Cie bardzo Miales oszczedzac wzrok

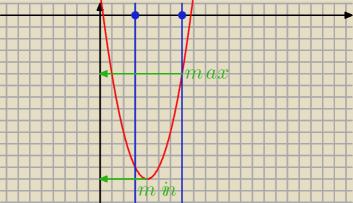
Pan K: nalezy sprawdzic czy wierzcholek paraboli nalezy do zadaniego przedzialu

	b		−8
xw= −		= −		=4 nalezy wiec minimum bedzie w wierzcholku
	2a		2

Teraz mozna sobie zrobic tak y=x²−8x+2 y=(x−4)²−14 jest to postac kanoniczna funkcji kwadratowej Stad odczytuje zbior wartosci funkcji Zw_f=<−14,∞) widac ze −14 to minimum (bo ramina w gore ) teraz policzyc f(3) i f(7) i wybrac maksimum

Jerzy: Lepiej zapisywać [3,7]