Wykaż, że równanie 1) x^3+3x-π=0 ma dokładnie jedno rozwiązanie ddd: Wykaż, że równanie 1) x³+3x−π=0 ma dokładnie jedno rozwiązanie 2) sinx=x−1 ma dodatni pierwiastek

janek191: x³ + 3 x − π= 0 f(x) = 3 x² + 3 > 0 więc funkcja g(x) = x³ +3 x − π jest rosnąca w ℛ zatem ma jedno miejsce zerowe.

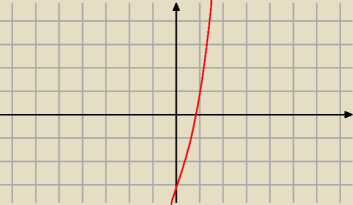
janek191: 1)

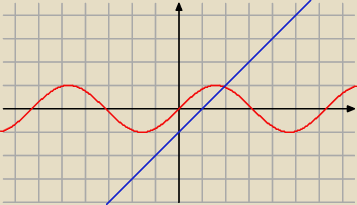
janek191: 2) sin x =x − 1 − 1 ≤ sin x ≤ 1 więc − 1 ≤ x − 1 i x − 1 ≤ 1 − x ≤ 0 i x ≤ 2 x ≥ 0 i x ≤ 2 x = 0 nie jest rozwiązaniem, więc x ∊( 0 , 2 >

Saizou : do pierwszego można zastosować tw. Sturma

ICSP: Drobna uwaga. Funkcja rosnąca w R nie musi mieć miejsca zerowego ( patrz np f(x) = 2^x )

ABC: a jeśli jest ciągła i idzie od minus do plus nieskończoności to już będzie miała z tym twierdzeniem Sturma to lekki overkill bym powiedział

6latek: A ja bym chcial zeby to pokazal Saizou . Kiedys o tym twierdzeniu czytalem

janek191: A ddd: nie interesują rozwiązania.

Jerzy: Wystarczy twierdzenie Darboux Funkcja jest stale rosnąca i f(0) = − π < 0 oraz f(1) = 4 − π > 0 Wniosek: funkcja posiada tylko jedno miejsce zerowe, należące do przedziału ([0,1]

janek191: Pięknie

Jerzy: @janek 191 , argumentacja : "funkcja jest rosnąca w R więc ma jedno miejsce zerowe" jest niewystarczająca.

janek191: Wiem