Stereometria- oblicz pole przekroju borówka : Podstawą graniastosłupa prostego jest romb o kącie ostrym mający miarę 60 stopni. Dłuższa Przekątna graniastosłupa ma długość D i jest nachylona do płaszczyzny podstawy pod kątem o mierze 45°. Graniastosłup przecięto płaszczyzną zawierającą dłuższą przekątną podstawy i środki dwóch boków górnej podstawy. oblicz pole otrzymanego przekroju. Bardzo prosze o pomoc! Doszłam do tego, ze przekrój jest trapezem i jego podstawy maja długość: pierwiastek z dwóch/2 * D i druga: pierwiastek z dwóch/4*D

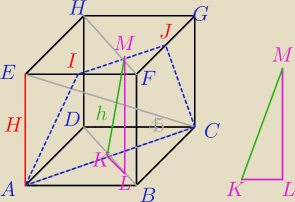
Saizou : |AE|=|AC|=H (ΔCAE jest równoramienny prostokątny) ΔIJD~ΔABC (cecha bkb) w skali 2:1

	1		1
|IJ|=		|AC|=		H
	2		2

	1
|KL|=		|BD| (BD można obliczyć z tw. cosinusów)
	4

|ML|=H i potem Pitagoras

borówka : Kurcze, a które kąty są takie same w tych dwóch trójkątach ΔIJD i ΔABC? Akurat zawsze mam problem z ustaleniem podobieństwa i teraz tez tego nie moge zobaczyć

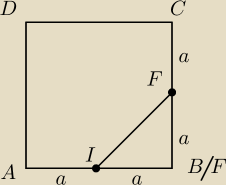
Saizou : a w takiej sytuacji to zobaczysz?

borówka : O Dziekuje! A w takim razie to nie ma być trojkat ΔIJF zamiast ΔIJD i jeszcze przepraszam bardzo, ale od razu sie spytam dlaczego akurat ten odcinek |KL| jest 4 razy mniejszy od |BD|?

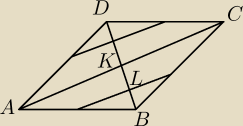
Saizou : Podobieństwo jest dobrze napisane, ja ci teraz narysowałem to na jednym poziomie abyś widziała co tam się dzieiej. Też z podobieństwa trójkątów to wynika albo z tw. Talesa. Pomyśl dlaczego tak

borówka : Dobrze, mysle ze teraz juz wszystko jasne! Jeszcze raz bardzo Dziekuje