FUNKCJE bluee: Niech f(x) = x² + 2x + 3 znalezc f([−2; 1)) oraz f⁻¹1((3; 6]). Czy to znaczy, że mam przedstawić zakres wartości funkcji dla x∊przedziałów w nawiasach? Czy f⁻¹=−1+√x−2 gdzie x∊<−2,∞) ?

6latek: masz znalezc obraz i przeciwobraz

bluee: Yyy... Powiem tak były takie zadanie na pierwszych ćwiczeniach z Algebry i geometrii. Jestem chora więc nie dotarłam na wykład. I teraz próbuję się odnaleźć Na każdym ćwiczeniem mam krótką informację. Tutaj była taka Dla A ⊂ X definiujemy f(A) = {y∊ Y : ∃x ∊2 A : f(x) = y} Dla B ⊂ Y definiujemy f⁻¹(B) = {x ∊ X : f(x) ∊2 B} Czytam podręcznik, ale to materiał rozpisany na 100 stronach. A zadania chcę odesłać jak najszybciej. Czy ktoś mógłby mi to wyjaśnić?

6latek: f(<−2,1)= <3,6) Obraz liczysz wartosc funkcji na koncach przedzialu Przeciwobraz f⁻¹ to liczysz jakie beda x_y dla danych y np tutaj dla y=3 3= x²+x+3 tutaj x=0 ale nie bedzie nalezec do przedzialu przeciwobrazu liczysz 6=x²+x+3 wylicz x

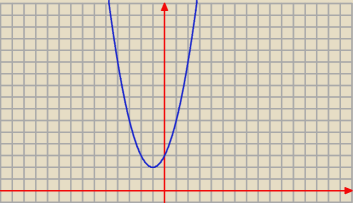
6latek: Z wykresu wszystko odczytasz 6=x²+2x+3 to x=1 f⁻¹(3,6>)= (0,1>

6latek: ja to tak mialem wytlumaczone w swojej ksiazce do 1 liceum Anusiak

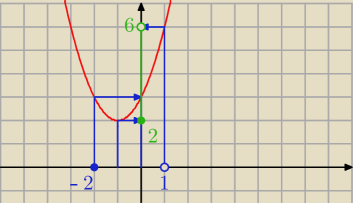
Saizou : f([a,b]) to obraz przedziału [a,b] przez funkcję f czyli szukasz y, które powstały w wyniku przekształcenia przedziału (czyli x−ów) Np. f(x)=x²+2x+3 f([−2,1))=[2, 6)

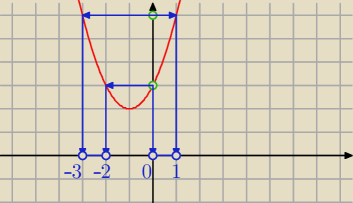
Saizou : Przeciwobraz, na odwrót, czyli szukasz x−ów f⁻¹((a,b)) to przeciwobraz przedziału (a,b) f⁻¹((3,6))=(−3, −2) ∪ (0, 1)

ite: Moim zdaniem przeciwobrazem przedziału (3,6] jest suma przedziałów [−3,−2)U(0,1].

Saizou : \N[ite]] zauważ że ja wziąłem innych przedział (obustronnie otwarty), dla prawostronnie domkniętego masz 100% rację

6latek: Kuz...a wzialem tylko jedna strone

ite: Widzę, że masz inny przedział : ) Moja uwaga była do niepełnej odpowiedzi z 13:08 (tylko za późno napisana).

6latek: dzien dobry ite

ite: Dzień dobry! Znajdowanie przeciwobrazu chyba jest mniej intuicyjne niż obrazu.

bluee: Hej, dzięki za wszystkie odpowiedzi. Mam jeszcze jedno pytanie czy funkcja przeciwna, która podałam na początku jest prawidłowa? To z zadania wcześniejszego, dlatego pytam.

Saizou : Jeśli chodzi o funkcje odwrotną to musi być ona bijektywna (czyli różnowartościowa i na). Funkcja f(x)=x²+2x+3 nie jest różnowartościowa w R. Obcinając ją do przedziału (−1:+∞) (albo do przedziału (−∞;−1)) możemy wyznaczyć funkcje odwrotną do niej y=x²+2x+3 y=x²+2x+1+2 y=(x+1)²+2 y−2=(x+1)² zał. y−2≥0→y≥2 √y−2=|x+1| (w zależności jaki przedział wybrałaś będą tutaj dwie wersje) x=√y−2−1 po zamianie zmiennych y=√x−2−1

bluee: Czy suriekcja oznacza, że funkcja jest ciągła?

Saizou : Nie

bluee: Funkcje f : X → Y nazywamy surjekcja wtedy i tylko wtedy, gdy ∀ y ∊ Y ∃ x ∊ X : f(x) = y Jaki jest przykład funkcji, ktora nie spełnia tego warunku?

Saizou : przykład f: R→Y f(x)=x² Y=[−1,1] f jest funkcją ciągłą, ale nie znajdziesz takiego x, że −1=x²

bluee: Funkcja o dziedzinie X i wartosciach w zbiorze Y nazywamy dowolny podzbiór f zbioru X x Y. Czyli zbiór XxY traktuję jako cały układ współrzędnych?

bluee: Źle postawiłam pytanie. Przyjmuesz określony zbiór Y i spawdzasz czy pokrywa się ze zbiorem wartości funkcji f? Jest tak to funkcja jest suriekcją jeśli nie to nie?

Saizou : Odp. Każda funkcja może być traktowana jako suriekcja na swój zbiór wartości, tzn. Y jest zbiorem wartości. Suriektywność funkcji zależy właśnie od wyboru zbioru Y