Dane są dwa przeciwległe wierzchołki kwadratu A=(1,-2) i C=(3,6). Wyznacz współr Kox: Dane są dwa przeciwległe wierzchołki kwadratu A=(1,−2) i C=(3,6). Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.

Saizou : Skorzystaj z wiedzy, że przekątne w kwadracie przecinają się pod kątem prostym i w połowie

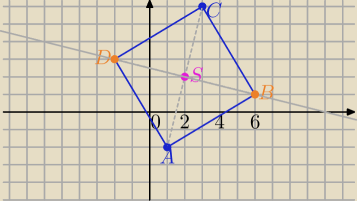
Mila: Jeden ze sposobów, z wykorzystaniem wektorów. Przekątne są prostopadłe, równej długości i przecinają się w połowie. A=(1,−2) i C=(3,6). S=(a,b)− środek AC

	1+3		−2+6
a=		=2, b=		=2
	2		2

S=(2,2) AS^→=[1,4] SB^→⊥AS^→ SB^→=[4,−1] S=(2,2)→T_[4,−1]⇒B=(2+4,2−1)=(6,1) B=(6,1) S=(2,2)→T_[−4,1]⇒D=(2−4,2+1)=−(−2,3) D=(−2,3) II sposób S=(2,2), przekątne są prostopadłe, równej długości i przecinają się w połowie. 1) BD− Symetralna odcinka AC: A=(1,−2) i C=(3,6). (x−1)²+(y+2)²=(x−3)²+(y−6)²⇔

	1		5
y=−		x+
	4		2

2) Równanie okręgu o środku S=(2,2) i r=|AC|=√1²+4², r=√17 (x−2)²+(y−2)²=17 3) punkty przecięcia okręgu i BD

	1		5
(x−2)2+(−		x+		−2)2=17
	4		2

stąd :

	1		5
x=−2 wtedy y=−		*(−2)+		=3
	4		2

D=(−2,3) lub

	1		5
x=6 wtedy y=−		*6+		=1
	4		2

B=(6,1) ===============