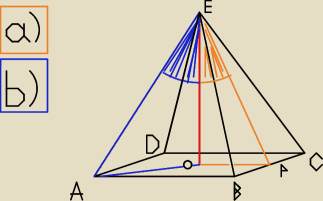
 Zadanie z polecenia:
a) cosα = 0,8=Hh
810=6h
8h=60 / :8
h=7,5
H2+|OP|2−h2
62+|OP|2−7,52
|OP|2=56,25−36
|OP|=√20,25
|OP|=12a
√20,25=12a / *2
Wynik: a=2√20,25 <−−−− co do tego wyniku to nie jestem pewien przez ten ułamek.
"""""""""""""""""""""""""""""""""""""""""""""""
b) cosα=310=H|EA|
310=6|EA|
3|EA|=30 / :3
|EA|=10
|EA|2+62=102
|EA|2=100−36
|EA|=√64
|EA|=8
8=12*a√2 / *2
16=a√2 / *√2
2a=16 / :2 2a bo √2*√2=2
a=8
Dobrze to zrobiłem?
Zadanie z polecenia:
a) cosα = 0,8=Hh
810=6h
8h=60 / :8
h=7,5
H2+|OP|2−h2
62+|OP|2−7,52
|OP|2=56,25−36
|OP|=√20,25
|OP|=12a
√20,25=12a / *2
Wynik: a=2√20,25 <−−−− co do tego wyniku to nie jestem pewien przez ten ułamek.
"""""""""""""""""""""""""""""""""""""""""""""""
b) cosα=310=H|EA|
310=6|EA|
3|EA|=30 / :3
|EA|=10
|EA|2+62=102
|EA|2=100−36
|EA|=√64
|EA|=8
8=12*a√2 / *2
16=a√2 / *√2
2a=16 / :2 2a bo √2*√2=2
a=8
Dobrze to zrobiłem?
| 1 | 81 | 9 | ||||
20.25 = 20 | = | = ( | )2 = (4.5)2 | |||
| 4 | 4 | 2 |