nie rozumiem ola: Wyznacz liczbę rozwiązań równania w zależności od wartości parametru m. W przypadku istnienia rozwiązań wyznacz je. |x−6|+|x+1|=8 Proszę o pomoc w jednej rzeczy: rozważam trzy przedziały: (∞,−1) , <−1,6), <6,∞) wyniki mam dobre, ale... gdy zapisuję: − brak rozwiązań jeśli m∊(−∞,7) − ma dwa rozwiązania jeśli m∊ <7,∞) −−−−− DLACZEGO TU PRZEDZIAŁ POWINIEN BYĆ NIEDOMKNIĘTY − ma nieskończenie wiele rozwiązań jeśli m=7 Proszę tylko o wytłumaczenie dlaczego te przedział nie możne być domknięty ?

Jerzy: Przecież w równaniu nie ma parametru.

ola: poprawka przepraszam |x−6|+|x+1|=m

ABC: dla m=7 masz nieskończenie wiele rozwiązań a skoro nieskończenie wiele to nie dwa dwa masz jak będziesz "ciut" wyżej niż 7

jj: ∞Δt

ola: jj: nie rozumiem ?

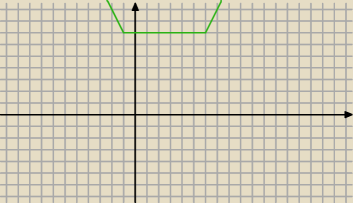
ABC: taki wykres ci wyszedł ?

ola: Dziękuję zrozumiałam

Mila: (1) |x−6|+|x+1|=m |x−6|+|x+1|=|x−6|+|−x−1|≥|x−6−x−1|=7 − najmniejsza wartość lewej strony równania (1) równość zachodzi dla x∊<−1,6>⇔ Równanie posiada nieskończenie wiele dla m=7.