Różnowartościowość funkcji
kam99: Zbadaj, które z podanych funkcji są różnowartościowe.
b) f(x) = 2
−x+3
6 paź 12:01
ABC:
obydwie są, i można dosyć prosto to udowodnić
6 paź 12:17
kam99: możesz mi pokazać na jednym przykładzie w jaki sposób ?
6 paź 13:24
ABC:
| x−1 | | x+1−2 | | 2 | |
| = |
| =1− |
| |
| x+1 | | x+1 | | x+1 | |
| | 2 | | 2 | |
Niech a,b ≠−1 oraz f(a)=f(b) czyli 1− |
| =1− |
| |
| | a+1 | | b+1 | |
| | 2 | | 2 | | 1 | | 1 | |
przekształcając mamy |
| = |
| , |
| = |
| , b+1=a+1 , b=a |
| | b+1 | | a+1 | | b+1 | | a+1 | |
czyli z f(a)=f(b) wynika a=b
6 paź 13:48
janek191:
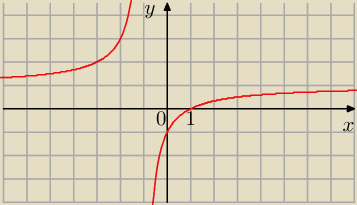
Wykres funkcji:
| | x − 1 | |
y = |
| , x ≠ − 1 |
| | x + 1 | |
6 paź 13:58
Jerzy:
I do czego mu potrzebny ten wykres ?
6 paź 14:00