Pytanie Rong Le:

	|x−1|
czy funkcja f(x)=		jest funkcja wymierna ?
	|x|−1

jc: Czy to jet iloraz wielomianów?

Rong Le: Zbyt trudne pytania zadajesz w sobote

Rong Le: Ok . Mam rozumiec tak Jesli w liczniku lub w mianowniku wystepuje wyrazenie z wartoscia bezwzgledna to taka funkcja nie ejst wymierna To samo bedzie jesli jednoczesnie w liczniku i w mianowniku wystepuja wartosci bezzgledne to takie wyrazenie nie jest wymierne . tak ?

Jerzy:

	1
Dobre pytanie. Czy np. funkcja: f(x) =		jest funkcją wymierną ?
	x

Jerzy: Przeczytaj uważnie definicję funkcji wymiernej.

Rong Le: Jerzy mam takie cwiczenie w ksiazce i sposrod wielu funkcji mam tylko ta jedna z wartoscia bezwzglena i pytanie jest wlasnie o nia

Rong Le: Funkcja wymierna jest to iloraz wielomianow jednej zmniennej

Rong Le: Po prostu |x|−1 nie jest wielomianem bo wielomian jednej zmiennej jest okreslony wzorem W(x)= a_0a1x+a₂x²+a₃x³+.....+ a_nxⁿ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− To juz wszystko wyjasnia .

Pan Kalafior: Machanie rękoma. Funkcje wymierne są ciągłe, a w punktach gdzie nie są określone, ich moduły dążą do ∞. Ta funkcja nie może więc być funkcją wymierną, bo granice w 1 ma ±1.

Rong Le: Dobre spostrzezenia Nie mialem jeszcze granic . dziekuje Ci .

Jerzy: Panie Kalafiorze,funkcja f(x) = 1/x nie jest ciągła,a jest funkcją wymierną.

Pan Kalafior: Jest ciągła.

Jerzy: A jaką przyjmuje wartość dla: x = 0 ?

Pan Kalafior: Żadną

Jerzy: No to jakim cudem jest ciągła ?

jc: Po prostu jest ciągła. Jaką masz definicję ciągłości? Może wg Twojej nie jest.

Jerzy: Racja, jest ciągła w swojej dziedzinie Teraz pytanie: czy funkcja stała jest funkcją wymierną ?

Rong Le:

	3
wedlug mnie tak bo np y=3=
	1

PW: Dyplomatyczna odpowiedź na postawione pytanie brzmi: Funkcja

	|x−1|
f(x) =
	|x|−1

jest kawałkami wymierna, tzn. jej dziedzinę można podzielić na kilka kawałków, tak że na każdym z nich jest to funkcja wymierna.

ABC:

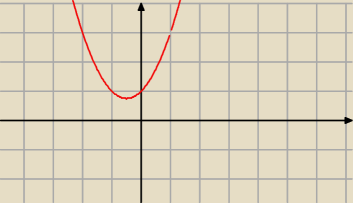
	x3−1
taka dygresja :to jest wykres funkcji wymiernej		więc to co napisano 5.X 20:58
	x−1

nie jest prawdą.

Pan Kalafior: Jest prawdą dla funkcji wymiernych f(x)/g(x), f, g wielomiany, g ≠ 0, nwd(f, g) = 1 To miał być zarys idei a nie dowód