proszę o pomoc bjkm: −x⁹ + 4x⁶ + 28x³ +32≥0

Mariusz: http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf −x⁹ + 4x⁶ + 28x³ +32=0 z=−x³ z³+4z²−28z+32=0 1 4 −28 32 −4/3 1 8/3 −284/9 2000/27 −4/3 1 4/3 −100/3 −4/3 1 0 −4/3 1

	4		100		4		2000
(z+		)3−		(z+		)+		=0
	3		3		3		27

	4
y=z+
	3

	100		2000
y3−		y+		=0
	3		27

y=u+v (u+v)³=u³+3u²v+3uv²+v³ (u+v)³=u³+v³+3uv(u+v)

	100		2000
u3+v3+3uv(u+v)−		(u+v)+		=0
	3		27

	2000		100
u3+v3+		+3(u+v)(uv−		)=0
	27		9

	2000
u3+v3+		=0
	27

	100
3(u+v)(uv−		)=0
	9

	2000
u3+v3=−
	27

	100
uv−		=0
	9

	2000
u3+v3=−
	27

	100
uv=
	9

	2000
u3+v3=−
	27

	1000000
u3v3=
	729

	2000		1000000
t2+		t+		=0
	27		729

	1000
(t+		)2=0
	27

	10
u=−
	3

	10
v=−
	3

	20
y=−
	3

	4		20
z+		=−
	3		3

	20		4
z=−		−
	3		3

z=−8 z³+4z²−28z+32=0 z³+8z²−4z²−32z+4z+32=0 z²(z+8)−4z(z+8)+4(z+8)=0 (z+8)(z²−4z+4)=0 (z+8)(z−2)²=0 Rzeczywiste miejsca zerowe wielomianu −x⁹ + 4x⁶ + 28x³ +32 to x₁=2 x₂=−³√2 x₃=−³√2 x∊(−∞,2>

WhiskeyTaster: Albo spróbuj najpierw szukać pierwiastków wymiernych.

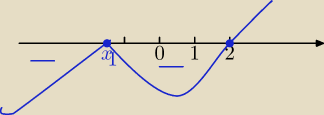
Mila: −x⁹ + 4x⁶ + 28x³ +32≥0⇔ (1) x⁹−4x⁶−28x³−32≤0 1) Podstawienie: x³=t t³−4t²−28t−32≤0 2) Szukamy pierwiastków wymiernych w(t)=t³−4t²−28t−32: w(±1)≠0 w(2)=8−16−56−32≠0 w(−2)=−8−16+56−32=0⇔t=−2 jest pierwiastkiem wielomianu w(t) Dzielimy w(t) przez (t+2): t=−2 1 −4 −28 −32 1 −6 −16 0 t³−4t²−28t−32=(t+2)*(t²−6t−16) Δ=100

	6−10		6+10
t=		lub t=
	2		2

t=−2 lub t=8 3) w(t)=(t+2)²*(t−8)²≤0⇔ (x³+2)²* (x³−8)≤0 (x³+2)²*(x−2)*(x²+2x+4)≤0 (x³+2)² ≥0 dla x∊R,(równe 0 dla x₁=−³√2) , x²+2x+4>0 dla x∊R (Δ<0) odp. x≤2

Mariusz: WhiskeyTaster: Jakoś nie chciało mi się sprawdzać tych pierwiastków bo to po pierwsze nie zawsze jest szybsze po wtóre nie daje gwarancji że pierwiastek znajdziemy

WhiskeyTaster: Mariusz, wiem o tym doskonale. Po prostu nie ma co się oszukiwać − przedstawiony przez Ciebie sposób jest ciekawy i chętnie go sobie przyswoję, więc dziękuję za podanie linku do PDFa, ale jednocześnie ta metoda może sprawić problem dużej części uczniów szkół średnich. A zadanie wygląda właśnie na ten poziom nauczania.