Monotoniczność funkcji trygonometrycznych salamandra: Czy ktoś wytłumaczyłby mi łopatologicznie monotoniczność funkcji trygonometrycznych (sin, cos, tg)? Mam podane że funkcja cos rośnie w przedziale (π + 2kπ ; 2π +2kπ) oraz że maleje w przedziale (0+2kπ; π+2kπ). Dlaczego w ogólnym wzorze nie ma na przykład podane −π (od tego momentu również funkcja cosinus rośnie)?

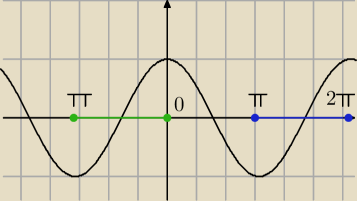
Saizou : po prostu wzięli inny przedział początkowy (ten niebieskie) a ty chcesz rozpocząć od zielonego przedziału, wynika to z okresowości biorąc k=−1 dla przedziału (π+2kπ; 2π+2kπ) otrzymamy (−π; 0)

salamandra: Ok, już chyba rozumiem, po prostu wziąć obojętnie jaki przedział, czyli na przykład (π; 2π), a to 2kπ, to po prostu okres, czyli de facto wrócimy do punktu wyjścia

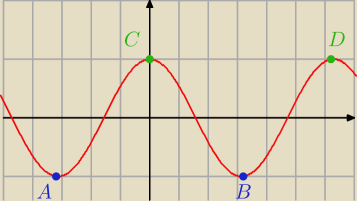
Saizou : obojętnie jaki, w którym cosinus jest rosnący Ja polecam taką metodę, że opisuję najpierw jedną "dolinę" (tutaj A) i patrzę i ile muszę się przesunąć, aby otrzymać dolinę B, czyli opisuję lewy koniec przedziału A=−π ale aby dojść do B muszę przejść o 2π w prawo czyli lewy koniec to −π+2πk Tak samo z górkami

salamandra: A mógłbym równie dobrze wyznaczyć wzór że cosinus rośnie w przedziale (−π+2kπ; 0+2kπ)?

Saizou : Tak, to bez znaczenia w jakim momencie zaczniesz

salamandra: czyli de facto nie ma czegoś takiego jak wzór ogólny, bo istnieje ich nieskończenie wiele, w zależności od tego w którym momencie zaczniemy?

Saizou : Nie ma jednoznacznego wzoru ogólnego, ale każdy z wzorów np. (π+2kπ; 2π+2kπ) czy też (−π+2kπ; 0+2kπ) opisuje te same przedziały, tylko żeby je uzyskać trzeba brać różne k Zad. dodatkowe Wyznać dla jakiego k, powyższe przedziały, są określone jako (9π, 10π)

salamandra: 4

salamandra: no ale w sumie zależy z którego wzoru korzystam

Saizou : Dokładnie tak, miało to na celu pokazać, że te dwa przedziału tak na prawdę będą opisywać te same rozwiązania, tylko dla odpowiedniego k

salamandra: Ok, dziękuję bardzo za pomoc