Funkcje odwrotne BAI PING TING: Zbuduj funkcje odwrotna do podanej nizej funkcji Dokonaj zamiany zmiennych i naszkicuj wykresy danej funkcji i funkcji do niej odwrotnej . Wskazowka Ustal przedzialy w ktorych dana funcja jest roznowartosciowa a) y=x³ x∊R b) y=√x−2 x∊<2,∞)

	1
c)		x∊R\{3}
	x−3

d) y=x² x∊R e) y=[x] x∊R f) y=2|x+1| x∊R Wykresy moze sobie daruje a) y=x³ musze wyznaczyc x x³= y x=³√y zamiana zmiennych y=³√x Teraz jak wyznaczyc te przedzialy roznowartosciowosci ?

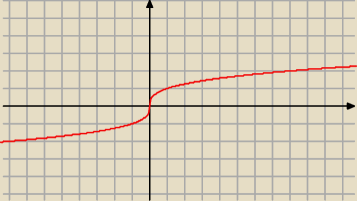
BAI PING TING: y=³√x bedzie roznowartosciowa dla x∊(−∞,∞)

BAI PING TING: Czy to na razie jest dobrze ?

Jerzy:

Jerzy: y = x³ jest różnowartościowa w całej dziedzinie.

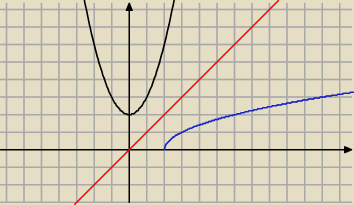
BAI PING TING: b) y=√x−2 x∊<2,∞) y²= x−2 y²+2=x x²+2=y Tutaj nie wiem co napisac o roznowartosciowosci Ze jest roznowatosciowa x∊<0,∞)

janek191:

BAI PING TING:

	1
c) y=		x∊R\{3}
	x−3

y(x−3)=1 yx= 3y−1

	3y−1
x=
	y

zamiana zmiennych

	3x−1
y=
	x

Funkcja odwrotna jest rownowatosciowa dla x∊R\{0}

BAI PING TING: dzien dobry janek191 Pada u Ciebie ?

janek191: Teraz już nie. Pozdrawiam

BAI PING TING: Wlasnie bylem na spacerze to padalo .Teraz przestalo

BAI PING TING: d) ogolnie to ta funkcja nie ma funkcji odwrotnej bo nie jest roznowartosciowa w calej dziedzinie Co tu zrobic? tak samo bedzie w e) i f) bo te funkcje tez nie sa roznowartosciowe

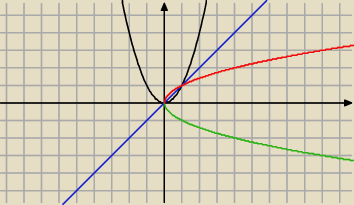
6latek: W e) chyba nic nie zrobie natomiast w d) i f) moze sprobowac przedzialami y=x² x∊<0,∞) x=√y y=√x ta funkcja bedzie roznowartosciowa x∊<0,∞) Ale tez y=x² jest roznowartosciowa dla x∊(−∞.0) (moge tutaj domknac to 0 czy juz nie ? Odwrotna to po zamanie zmiennych y=−√x i x∊<0,∞) Tutaj byloby dobrze

Jerzy: Ograniczyć dziedzinę.

6latek: Jerzy f) juz mam zrobione w e ) nie znajde takiego przedzialu

Jerzy: Zauważ,że wykres funkcji odwrotnej jest symetryczny do danej względem prostej y = x i popatrz na wykres funkcji f(x) =[x]

6latek: OK.