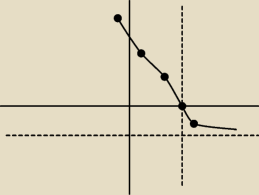
Funckja wykładnicza Matus126: Punkt (−2,4) należy do wykresu funkcji wykładniczej f(x)=a^x dla x∊R a)Wyznacz a i zapisz wzór funkcji g otrzymanej w wyniku przesunięcia wykresu funkcji f o wektor u = [2,−1] b)Narysuj wykres funkcji c)Odczytaj z wykresu zbiór wszystkich argumentów dla których g(x)>0 Chciałbym sprawdzić czy dobrze zrobiłem a) f(x)=a^x i A=(−2,4) 4=a⁻2 N{1]{a²}=4 / a² 1=4a² / :4 a²=1/4 a=1/2 lub a=−1/2 odrzucamy a=−1/2 ponieważ funkcja wykładnicza musi być >0

	1 2
b)g(x)=(		)x−2 − 1

c)g(x)>0 dla x∊(0,∞) Rysunek byle jaki , ale chodzi o funkcje czy dobrze napisana ponieważ wiem jak się rysuje , bardziej chodzi mi o asymptoty że czy dobrze jest że obnizona oś X o jedno w dól , a oś Y o dwa w prawo

ABC: punkt c) nie jest dobrze zrobiony

Matus126: W sensie jaki powinna być prawidłowa odpowiedz ?

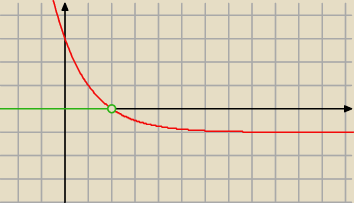
ABC: tam gdzie zielone

Matus126: Nie rozumiem w sumie ponieważ gdy g(x)>0 to bierzemy z osi Y więc z twojego rysunku widzę przedział od (−∞,2) to jest poprawna odpowiedz ? Bo mi się już wszystko pomieszało

ABC: miałeś w poleceniu zbiór ARGUMENTÓW czyli (−∞,2)

BAI PING TING: g(x) to sa wartosci funkcji np dla x=2 wartosc funkcji jest ujemna (odczytujesz na osi OY dla x=0 g(x)=3>0

Matus126: Teraz to ma wszystko sens dziękuję bardzo !