Dowod BAI PING TING: Udowodnij twierdzenie ∃a,b∊R (a²+b²≤2 ⇒|a+b|≤2) Wskazowka 2a²+2b²= (a+b)²+(a−b)² Nie wiem jaki do tego podejsc Zadanie z cyklu trudnych

ICSP: |a + b| = √ (a+b)² ≤ √(a+b)² + (a−b)² = ...

Pan Kalafior: a = b = −1

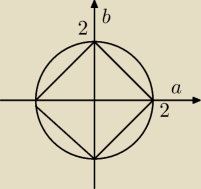
jc: Nierówność mówi, że kwadrat leży wewnątrz koła.

PW: Ten kwantyfikator „∃” jest mało sensowny.

BAI PING TING: W ksiazce jest ⋀ab∊R ale chyba to to samo

Mila: ⋀ dla każdego.... ∃ istnieje ..... ∀ istnieje.....

BAI PING TING: napisze rozwiazanie z ksiazki (zagladnalem do odpowiedzi a²+b²≤2⇒2a²+2b²≤4⇒(a+b)²+(a−b)²≤4 (a+b)²≤(a+b)²+(a−b)² Z tych powyzszych nierownosci wynika ze (a+b)²≤4 stad |a+b|≤2 Powiem ze srednio to rozumiem oprocz samej koncowki

BAI PING TING: Dobry wieczor Milu pozdrawiam Moze Ty rozpiszesz mi ten dowod abym to zrozumial

ICSP: Mila, nie do końca. Notacja Polska: ∧ − dla każdego ∨ − istnieje Notacja zagraniczna: ∀ − dla każdego ( odwrócona litera a od słowa all) ∃ − istnieje ( odwrócona litera e od słowa exists )

Mila: 1) "Rozpisuję" (a²+b²≤2 ⇒|a+b|≤2) a²+b²≤2 /*2 ⇔ 2a²+2b²≤4⇔ a²+2ab+b²+a²−2ab+b²≤4⇔ (a+b)²+(a−b)²≤4 (a+b)²≤(a+b)²+(a−b)²≤4⇔ (a+b)²≤4 |a+b|≤2 ======

Mila: Dzięki ICSP, nie jestem na bieżąco (?).

BAI PING TING: Dziekuje Ci Milu Bedziesz miala za to niebo To ja pomylilem oznaczenia .Dede pisal w notacji polskiej to nie bedzie pomylki

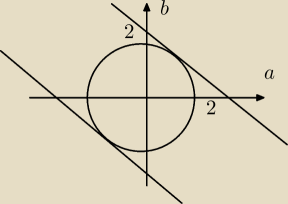
jc: To był zły rysunek. Nierówność mówi, że koło o promieniu √2 mieści się w pasie pomiędzy dwiema prostymi.