Funkcje BAI PING TING: Zadanie oznaczone w zbiorze jako bardzo trudne Tresc: Dane sa dwie funkcje f(x) i g(x) obie okreslone w tej samej dziedzinie D Sformuluj warunek konieczny i dostateczny na to aby a) wykresy tych funkcji byly symetryczne wzgledem prostej o rownaniu y=k b) wykresy tych funkcji byly symetryczne wzgledem prostej o rownaniu x=p Na razie to

jc:

	f(x)+g(x)
(a)		=k
	2

(b) f(p−x)=g(p+x)

jc: Podobają mi się zadania. W jakim zbiorze można je znaleźć?

BAI PING TING: https://zapodaj.net/1e34039bab6d0.jpg.html https://zapodaj.net/c9280a04dd085.jpg.html (ten wez po 1973 bo z 1973 jest duzo bledow

BAI PING TING: jc A jakies wyjsnienie do tego co napisales

jc: (a) f(x) . k . g(x) punkt k leży pośrodku, pomiędzy f(x) a g(x). (b) p−x ....... p ....... p+x Punkt p leży pośrodku, pomiędzy p−x a p+x.

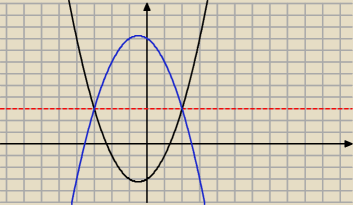
BAI PING TING: Mam podana funkcje f(x)= x²+x−3 Podaj wzor funkcji ktorej wykres jest symetryczny a) wzgledem prostej y=3 b) x=2

	f(x)+g(x)
a)		=3
	2

f(x)+g(x)= 3k g(x)= 3k−f(x) g(x)= 6−(x²+x−3)= −x²−x+9 ========================

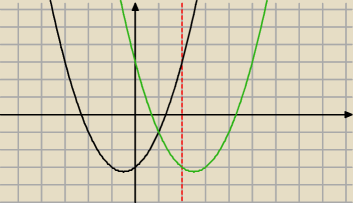
BAI PING TING: b) x=p x=2 to p=2 g(p+x)= (2−x)²+2−x−3 g(p+x)= x²−4x+4−x−1 g(p+x)= x²−5x+3 ================