wzajemne polozenie dwoch okregow Tłumok: podaj liczbę punktów wspólnych okręgu opisanego podanym równaniem z okręgiem o środku S(1,3) i promieniu r w zależności od tego promienia. a) x²+y²+4x+2y+1=0

Maciess: Najpierw sobie wzór przekształć do postaci z ktorej odczytasz współrzędne środka tego okręgu

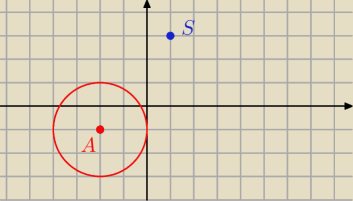
Saizou : x²+y²+4x+2y+1=0 x²+4x+4−4+y²+2y+1=0 (x+2)²−4+(y+1)²=0 (x+2)²+(y+1)²=4 zatem A=(−2,−1) oraz r₁=2 Pomyśl o liczbie przecięć się dwóch okręgów w zależności od r

Tłumok: skad mam wiedziec jaki promien ma okrag o srodku S... to polecenie jest takie pogmatwane

BAI PING TING: Bo mmasz podane rownanie okregu w postaci ogolnej jak przeksztalcic do postaci kanonicznej to co zrobli Saizou to masz wszystko na tacy Zreszta z postaci ogolnej tez policzysz zobacz do ksiazki jaki jest wzor na promien okregu

promując_geogebrę: https://www.geogebra.org/graphing/dyfz7x42

janek191: Oblicz AS r + r₁ = AS

Tłumok: ale to co obliczyl Saizou to chyba do okregu o srodku A?

janek191: Tak Ale piękna ta animacja

BAI PING TING: Tak

promując_geogebrę: Może pozwoli zobaczyć zagadnienie i samodzielnie znaleźć rozwiązanie.

Tłumok: wow dziekuje za animacje