prawdopodobieństwo Nikto0: Proszę o pomoc. W turnieju szachowym uczestniczy 10 zawodników. Każdy gra z każdymjeden raz figurami białymi i jeden raz czarnymi Wobec tego rozegrają a)90 partii b) 20 partii c)100 partii d) 45 partii. Ja zrobiłam to drzewkiem od 1 zawodnika mam 9 odgałęzień od 1 do 9 z tych odgałęzień do każdego partia grana czarnymi i białymi to wychodzi 18 mnożę przez 10 i dzielę przez 2. Czy to dobre rozwiązanie? To zadanie można też rozwiąza'ć za pomocą wariacji bez powtórzeń ale nie wiem dlaczego bo według mnie wszystkie elementy zostały wykorzystane. Może ktoś napisaćdlaczego to jest liczone z wariacji bez powtórzeń?

xyz:

	10 2
rozegrają		= 45 partii

janek191:

10 2
	*2

xyz: racja... * 2 bo 2 razy każdy z każdym

Nikto0: W odpowiedziach mam 90 partii xyz

Nikto0: A to drzewkiem to jest źle?

xyz: chyba jest ok, tylko musialbys wyjasnic czemu mnozysz razy 10 albo dzielisz przez 2

Nikto0: Mnożę razy 10 bo jest 10 zawodników a dzielę przez 2 żeby nieistotna była kolejność meczy.

Nikto0: To jest źle?

janek191: 10*9 = 90

Nikto0: To drzewkiem to chyba jest źle?

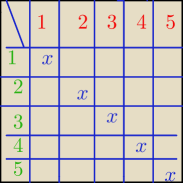
janek191: Masz narysowane dla n = 5 zawodników. Mamy 5*4 = 20 meczy Dla n = 10 mamy 10*9 = 90 meczy ( mecz i rewanż)

Nikto0: A jakiś opis tej tabelki?

janek191: 1 gra z 2, 3, 4 i 5 2 gra z 1,3, 4 i 5 3 gra z 1,2, 4 i 5 4 gra z 1,2,3 i 5 5 gra z 1,2,3 i 4

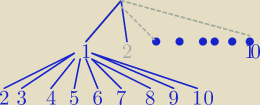
Mila: Drzewkiem też dobrze, ale tylko częściowe rysujemy. 10 *9=90 10 gałązek w I piętrze ( np. Białe pionki) i po 9 w drugim. W takich zadaniach, gdzie jest dużo gałązek raczej nie korzystamy z drzewek.

Nikto0: A dlaczego w tym przykładzie nie wszystkie elementy są wykorzystane ? Mi się wydaje że są wszstkie elementy wykorzystane?

Nikto0: Ok. To już rozumiem. Ale mam inne pytanie czy elementy mogą się powtarzać w tym przykładzie? I dlaczego?

Nikto0: Proszę o wyjaśnienie.

Mila: Gracz A gra z graczem B ( b , c− pionki) , a potem gracz B z graczem A innym kolorem niż w pierwszej partii. Nie może grać gracz A z graczem A. Zatem bez powtórzeń.

Nikto0: Dziękuję.

Saizou : Można też podejść inaczej. Ile możesz utworzyć par graczy? W parze nie ma znaczenia kolejność, tzn. para AB jest taką samą parą co BA

	10 2		10*9
Takich par jest		=		=45
			2

Ale teraz w każdej parze są rozgrywane dwa mecze. Raz zawodnik A gra czarnymi i B gra białymi lub na odwrót. Łącznie partii zostanie rozegranych. 45*2=90

Jerzy: To już pokazał @janek191 o 16:48

Saizou : Jerzy wiem, ale dopisałem do tego wyjaśnienie jeśliby ktoś potrzebował

Saizou : Albo można tak rozumować Wybieramy najpierw graczy, którzy będą grać białymi. Możemy to zrobić na 10 sposobów. Dobieramy, kto będzie grać białymi. Takich opcji jest 9 (bo nie gramy sami ze sobą) Razem 10*9=90

Nikto0: A dlaczego w filmiku Matemaksa dzieli on na dwa bo nie ma znaczenia kolejność czy tu też nie należałoby wykonać podzielenia? https://www.youtube.com/watch?v=I4nr92-92xY&t=413s w minucie 23:13

Nikto0: Poza tym w odpowiedziach jest to liczone wariacją bez powtórzeń a z tego grafu wynika że należy to zrobić z kombinacji http://www.math.edu.pl/images/algebra/kombinatoryka.gif

Nikto0: Ostatnie pytanie już rozumiem.

Nikto0: Jednak nie rozumiem tego zagadnienia

Jerzy: 11:02 Nie widzisz,że kombinacje: (ABCD) i (EFGH),to te same kombinacje co: (HGEF) i (DBAC) ?

Nikto0: tak widzę ale czy w tym zadaniu o turnieju szachowym też chyba nie liczy się kolejność

Nikto0: A nie dzielimy przez 2

Jerzy: W zadaniu o 10 szachistach liczymy ilość spotkań. Sa to dwuelementowe kombinacje zbioru

	10 2
dziesiecioelementowego, czyli		.Tyle będzie spotkań, ale kazdy gracz gra raz białymi, a

	10 2
raz czarnymi, czyli każda para rozegra dwa spotkania, stąd mamy:		*2 , więc o jakim

dzieleniu mówisz ?

Nikto0: bo mi się wydawało że w symbolu newtona 10 nad 2 zlicza się wszystkie przypadki czyli para AB to to samo co BA i dlatego dzielimy przez 2

Jerzy:

	10 2
Oczywiście,ze para AB to to samo co para BA , bo to są kombinacje i takich par jest		.

Nikto0: A nie powinno być tylko para AB bez BA

Nikto0: nie rozumiem tego

Jerzy: Wypisz dwuelementowe kombinacje zbioru {A,B,C}

Nikto0: {AB} {AC} {BC}

Jerzy: A czemu nie dodałaś (BA) ,(CA) , (CB) ?

Nikto0: sugerowałam się tym https://matematykaszkolna.pl/strona/1015.html

Nikto0: ale źle to zrozumiałam

Jerzy: A no właśnie. mamy trzy kombinacje , ale 6 permutacji bez powtórzeń, oraz 8 permutacji z powtórzeniami.

Nikto0: co to są permutacje z powtórzeniami?

Jerzy: W tym przypadku, każdy ciąg dwuelementowy, w którym wyrazy mogą się powtarzać: AA , BB , CC , AB , BA , AC , CA , BC , CB i jest ich dziewięć( przez pomyłke napisałem,ze jest ich 8)

Nikto0: I co z tego wynika?

Jerzy: Że w kombinacjach kolejność elementów jest nieistotna, czyli kombinacja AB , to to samo co kombinacja BA, natomiast AB i BA to dwie różne permutacje.

Nikto0: dalej niestety nie rozumiem o co chodzi.

Jerzy: Poczytaj to: https://matematykaszkolna.pl/strona/3425.html

Nikto0: Możesz to jakoś lepiej wyjaśnić?

Saizou : Wg mnie mylisz pojęcie kombinacji z regułą mnożenia Mamy 10 graczy i chcemy policzyć ile będzie meczów. Pierwszą osobę z pary mogę wybrać na 10 sposobów, a drugą na 9 (bez tej pierwszej), zatem łącznie mamy 10*9 Nie ma to znaczenia czy zawodnik A będzie grać z B, czy na odwrót, tzn. B z A. Dla nas jest to taka sama para. zatem musimy podzielić przez 2 i mamy

10*9
	(tyle jest par jakie możemy utworzyć).
2

Inaczej zapiszemy to przy pomocy symbolu Newtona. Jest to zwykły wybór 2 osób z 10, tzn.

10 2		10!		10*9
	=		=		.
		(10−2)!*2!		2

Teraz wiemy, że w każdej parze każdy z graczy gra raz białymi, a raz czarnymi, tzn. w obrębie pary odbywają się dwa mecze, dlatego mnożymy razy dwa.

10*9
	*2=10*9=90
2

Nikto0: dlaczego mnożymy przez 2 czy to nie jest już zliczone że zawodnik A gra z B np. białymi a potem B z A np.czarnymi

Saizou :

	10*9
Nie, bo zapis		mówi, że kolejność nie ma znaczenia.
	2

czyli para AB jest taką samą parą co BA

Jerzy: Napij sie wody. Jeżeli grasz z koleżanką w szacy raz białymi, a raz czarnymi bierkami,to ile rozegracie partii ?

Nikto0: dwie

Jerzy: A zatem 45 par uczestników rozegra 2*45 = 90 partii.

Nikto0: Dziękuję.