Proszę napiszcie z czego tu należy skorzystać
BB: Jak się do tego zabrać
W trójkącie równoramiennym w którym odcinek AC = BC, kąt c =120 stopni wpisano okrąg którego
promień jest równy 3 cm. Oblicz długości boków trójkąta
28 wrz 21:53
===:
Zrobić porządny rysunek

28 wrz 22:01
BB: Podpowiedzcie na co zwrócić uwagę
28 wrz 22:07
Eta:
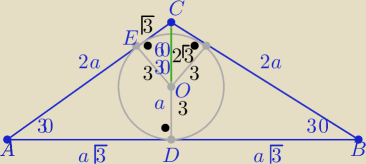
Z trójkątów "ekierek" o kątach ostrych 30
o, 60
o
W ΔADC : |AC|=|BC|=2a, |AB|=2a
√3 , |DC|=a
w ΔOEC :
|OC|=2{3}
to |CD|=|OD|+|OC| = 2
√3+3 =
a
zatem
|AC|=|BC|=2a=.............
|AB|=2a
√3=.................
dokończ obliczenia
28 wrz 22:08
===:
masz trójkat równoramienny. wysokość opuszczona na AB to zarazem dwusieczna kąta
jak i srodkowa. Kąty masz fajniutkie ... środek okregu dxzieli srodkową ... stosunek znasz.
Wysokość już tez znasz itd

28 wrz 22:14
Eta:

28 wrz 22:17
BB: Coś tego nie jarzę
28 wrz 22:21
xyz:
z wlasnosci trojkata ekierkowego
(o katach 30,60,90) znajac jeden bok, znasz pozostale dwa.
dlatego |OC| = 2√3 (bo znasz odcinek |OE| co wynosi 3 bo to promien
28 wrz 22:22
BB: Załapałem wielkie dzięki za pomoc
28 wrz 22:29
Eta:

28 wrz 22:47
Mila:
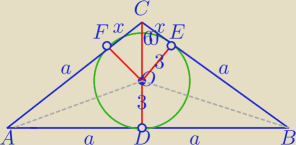
Z zastosowaniem f. tryg.
1) W ΔCEO:
|OC|
2=3
2+(
√3)
2
|OC|=2√3
2)
|CD|=3+2
√3
W ΔCDB:
| | a | | a | |
tg60o= |
| ⇔√3= |
| |
| | |CD| | | 3+2√3 | |
a=3√3+6
3) AB|=12+6
√3
|AC|=BC|=3
√3+6+
√3
|AC|=BC|=6+4
√3
==============
28 wrz 22:58
Eta:

28 wrz 23:41

 Z trójkątów "ekierek" o kątach ostrych 30o, 60o
W ΔADC : |AC|=|BC|=2a, |AB|=2a√3 , |DC|=a
w ΔOEC : |OC|=2{3}
to |CD|=|OD|+|OC| = 2√3+3 = a
zatem
|AC|=|BC|=2a=.............
|AB|=2a√3=.................
dokończ obliczenia
Z trójkątów "ekierek" o kątach ostrych 30o, 60o
W ΔADC : |AC|=|BC|=2a, |AB|=2a√3 , |DC|=a
w ΔOEC : |OC|=2{3}
to |CD|=|OD|+|OC| = 2√3+3 = a
zatem
|AC|=|BC|=2a=.............
|AB|=2a√3=.................
dokończ obliczenia



 Z zastosowaniem f. tryg.
1) W ΔCEO:
Z zastosowaniem f. tryg.
1) W ΔCEO:
