Geometria analityczna Marzenka: punkty K(2,1) L(3,3) M(02) sa srodkami bokow trojkata. oblicz wepolrzedne wierzcholkow tego trojkata. uzasadnij ze trojkat ten jest ro2noramienny.

janek191: A=( a,b) B = ( c, d) C = ( e, f) więc mamy

a + c		b + d
	= 2 i		= 1
2		2

to a + c = 4 i b + d = 2 oraz

c + e		d + f
	= 3 i		= 3
2		2

to c + e = 6 i d + f = 6 oraz

a + e		b + f
	= 0 i		= 2
2		2

to a + e = 0 i b + f = 4 Mamy układ 6 równań z 6 niewiadomymi. Obliczamy a,b,c,d,e,f Otrzymujemy współrzędne punktów A, B i C. Obliczamy długości boków ΔABC.

piotr: a = −1, b = 0, c = 5, d = 2, e = 1, f = 4

piotr: długości boków: (2√10 | 2√5) | 2√5)

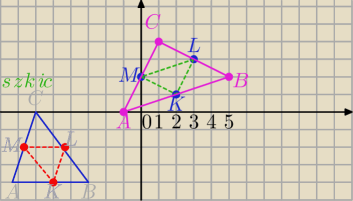
Mila: K=(2,1) L=(3,3) M=(0,2) Z lewej strony na dole szkic pomocniczy: 1) AB ||ML i |AB|=2*|ML| ML^→=[3,1] K=(2,1)→T_[3,1]⇒B=(2+3,1+1)=(5,2) K=(2,1)→T_[−3,−1]⇒A=(2+(−3),1+(−1)=(−1,0) A=(−1,0), B=(5,2) 2) BC||MK i |BC|=2*|MK| KM^→=[−2,1] L=(3,3)→T_[−2,1]⇒C=(3+(−2),3+1)=(1,4) C=(1,4) 3) Sama uzasadnij, że trójkąt jest równoramienny.

Mila: ?