zbiór wartości funkcji Paweł: Podaj zbiór wartości funkcji. Dla jakiego argumentu funkcja przyjmuje swoją wartość najwiekszą lub najmniejszą? a) y = −2(x+1)² + 5 b) y = 3(x−1)² −7 c) y = ¹₂(x − π) + 2 d) y = −2√7(x+3)² − 1 e) y = −4(x + ¹₂)² − 3 f) y = 0,2(x−2)²

Paweł: Proszę o szybką i skuteczną pomoc

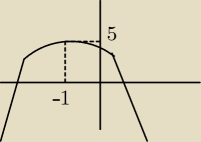
ula: musisz w każdym z tych równań skorzystać z równania paraboli y=a(x−p)²+q gdzie wierzchołek to (p,q) p to argument x a q to wartości funkcji np. a/ max dla argumentu (x) −1 zbiór wartości to y∊(−∞,5>

Paweł: czyli rozwiązania bedą następujące: b) ZW = (−∞; −7> wartość najmniejsza dla x=1 c) ZW = (−∞; 2> wartość najmniejsza 2 dla x = π d) ZW = (−∞; −1> wartość największa −1 dla x = −3 e) ZW = (−∞; −3> wartość największa −3 dla x = − ¹₂ f) ZW = (−∞; 0> wartość najmniejsza 0 dla x = 2

ula: pamiętaj o tym, że jeśli a jest ujemnie <0 to ramiona są skierowane do dołu (tak jak przykład a,d,e i wtedy ZW jest (−∞, q> q jest wartością największą (max) jeśli jednak a>0 to ramina są skierowane do góry więc ZW=<q, ∞) q jest wartością najmniejszą (min)

Paweł: czyli rozwiązania są dobrze?