z góry dzięki Heniu: Wykaż że jeśli D,E,F są rzutami prostokątnymi dowolnego punktu wewnętrznego P trójkąta równobocznego ABC odpowiednio na boki BC,CA,AB tego trójkąta, to zachodzi równość

	PD+PE+PF		√3
		=
	BD+CE+AF		3

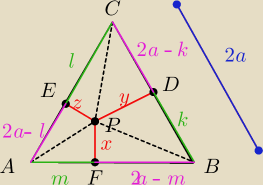
Saizou : Pokażemy najpierw, że PD+PE+PF= a√3. (wysokość trójkąta równobocznego o boku 2a)

	1
PABP=		•2ax=ax
	2

	1
PBPC=		•2ay=ay
	2

	1
PAPC=		•2az=az
	2

	1
PABC=		•2a•a√3=a2√3
	2

a²√3=ax+ay+az a√3=x+y+z Pokażemy teraz, że BD+CE+AF=3a Z twierdzenia Pitagorasa w odpowiednich trójkątach mamy, że (2a−m)²+x²=k²+y² (2a−k)²+y² =l²+z² (2a−l)²+z²=m²+x² ================= gdy to dodamy stronami i uprościmy mamy 12a²−4a(k+l+m)=0 k+l+m=3a zatem

PD+PE+PF		a√3		√3
	=		=
BD+CE+AF		3a		3

Heniu: Dzięki wielkie