Eta:
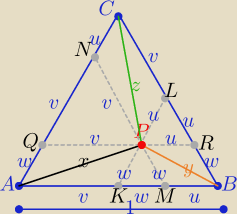
1/ rysunek na którym prowadzimy odcinki KL, MN, QR przechodzące przez punkt P
i równoległe odpowiednio do boków AC, BC, AB
otrzymujemy podział trójkąta ABC na trzy trójkąty równoboczne i trzy równoległoboki
2/ x,y,z <AB=1 czyli x,y,z∊(0,1)
to x
2+y
2+z
2<x+y+z
teza: x
2+y
2+z
2<2
3/ to należy teraz tylko wykazać,że x+y+z=2
Z nierówności trójkąta:
x<AK+KP =AK+KM = v+w ( bo ΔKMP −− równoboczny
y<BR+RP= ..... = w+u
z<CL+PL =... = v+u
to
x+y+z= 2v+2w+2u = 2(v+w+u)=2*1=2
zatem mamy tezę:
x
2+y
2+z
2<2
c.n.w.
 1/ rysunek na którym prowadzimy odcinki KL, MN, QR przechodzące przez punkt P
i równoległe odpowiednio do boków AC, BC, AB
otrzymujemy podział trójkąta ABC na trzy trójkąty równoboczne i trzy równoległoboki
2/ x,y,z <AB=1 czyli x,y,z∊(0,1)
to x2+y2+z2<x+y+z
teza: x2+y2+z2<2
3/ to należy teraz tylko wykazać,że x+y+z=2
Z nierówności trójkąta:
x<AK+KP =AK+KM = v+w ( bo ΔKMP −− równoboczny
y<BR+RP= ..... = w+u
z<CL+PL =... = v+u
to
x+y+z= 2v+2w+2u = 2(v+w+u)=2*1=2
zatem mamy tezę:
x2+y2+z2<2
c.n.w.
1/ rysunek na którym prowadzimy odcinki KL, MN, QR przechodzące przez punkt P
i równoległe odpowiednio do boków AC, BC, AB
otrzymujemy podział trójkąta ABC na trzy trójkąty równoboczne i trzy równoległoboki
2/ x,y,z <AB=1 czyli x,y,z∊(0,1)
to x2+y2+z2<x+y+z
teza: x2+y2+z2<2
3/ to należy teraz tylko wykazać,że x+y+z=2
Z nierówności trójkąta:
x<AK+KP =AK+KM = v+w ( bo ΔKMP −− równoboczny
y<BR+RP= ..... = w+u
z<CL+PL =... = v+u
to
x+y+z= 2v+2w+2u = 2(v+w+u)=2*1=2
zatem mamy tezę:
x2+y2+z2<2
c.n.w.