Kwadraty tomek: Hej, zastanawiało mnie czy mogę jakoś w matematyczny sposób rozłożyć kwadrat, np o boku n na mniejsze kwadraty, niekoniecznie identyczne. Wiem że mogę wziąć kartkę papieru i próbować to narysować czy coś ale mnie interesuje bardziej matematyczna strona tego problemu, tzn czy są jakieś własności czy równania odnośnie tego zagadnienia

Bleee: Jeżeli nie masz żadnych ograniczeń co do wielkości Ci mniejszych kwadratów, i ich ilości to wystarczy zauważyć że n² − (n−1)² = 2n − 1 Czyli robisz jeden kwadrat o jednostkę długości krótszym boku i dokladasz 2n−1 jednostkowych kwadracikow

tomek: A z czego wynika ta własność?

Jerzy: Za wzoru: a² − b² = (a + b)(a − b)

ite: 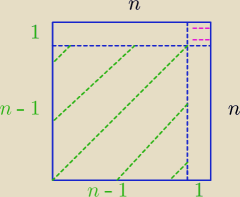(n−1)² + n*1 + n*1 − 1 = n² (n−1)² + 2*n*1 − 1 = n² 2*n*1 − 1 = n² − (n−1)²

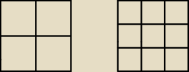
Pytający: Dla każdego kwadratu jest nieskończenie wiele różnych "rozłożeń" na mniejsze kwadraty... przykładowo dla każdej liczby naturalnej n>1 istnieje podział kwadratu na n² równych kwadratów (na rysunku dla 2, 3). Chyba że narzucasz jakieś ograniczenia (np. jedynie naturalne długości boków), wtedy może być inaczej... acz w takim przypadku wypadałoby doprecyzować swe pytanie Tomku.

tomek: dzięki wszystkim za odpowiedzi. Wiem że liczby które pozostają całkowite po podniesieniu do kwadratu, (3−>9, 4−>16) łatwo go dzielą na inne, identyczne i mniejsze, ale czy da się podzielić kwadrat np na 6 lub więcej różnych kwadratów, niekoniecznie identycznych? Czy jest na to jakiś algorytm?

Bleee: Doprecyzuj pytanie. Jakie wytyczne. W zależności od wytycznych algorytm może istnieć bądź może nie istnieć. Zb7t ogólnie postawiony problem

Pytający: Nie da się podzielić kwadratu jedynie na 2, 3, 5 mniejszych kwadratów. Zerknij tu: https://math.stackexchange.com/questions/1688313/a-square-cant-be-divided-into-2-3-or-5-smaller-squares https://math.stackexchange.com/questions/452252/proving-that-a-square-can-be-divided-into-n-smaller-squares-for-n-ge-6 Problem B: https://www.unomaha.edu/college-of-arts-and-sciences/mathematics/_files/docs/pow/S2018/Problem%205%20Solution.pdf

Pytający: Przy czym mowa o podziale na niekoniecznie różne kwadraty.

tomek: właśnie o to mi chodziło dziękuje bardzo