punkty w układzie xyz Peter: Witajcie, Na początek zadanie główne (opis): Wyobrażamy sobie układ 3D(xyz), mam tam tak na prawdę dwie kule punktów po obwodzie, czyli masa punków(takie dwie sfery) o wspólnym środku. Wybieram dwa punkty(przeciwstawne dla siebie względem środka) i mam wirtualną prostą. Teraz muszę znaleźć z innych punktów najbliższej położą inną prostą. Posiadam tylko współrzędne tych punktów(wszystkich) Tak więc jak miałbym tylko jedną kule(sferę) to lecę ze wzoru na odległość punktów 3D w koncepcji do 2 punktów (wyobraźmy sobie na dole i na górze) Ale jak mam dwie sfery(większą i mniejszą) to jest problem, bo prosta z dużej sfery może być prostą z małej sfery, ale jeżeli będę porównywał na zasadzie odległości tych punktów to wyjdzie że są daleko. Tak więc wymyśliłem, że muszę sobie wyliczyć nowy punkt na prostej z dużej sfery, który będzie leżał na małej sferze. Czyli muszę wyliczyć (poznać jego współrzędne) punkt między dwoma innymi punktami, który jest w określonej przeze mnie odległości od np. punktu pierwszego. Ktoś coś pomoże ? Mam nadzieję że nie zagmatwałem za bardzo, ale może ktoś wpadnie na jakiś inny łatwy pomysł. Zadanie do implementacji na kompie tak więc liczy się to aby komputer szybko liczył

Adamm: nic nie rozumiem

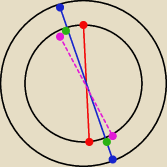
Peter: To jest coś takiego jak na rysunku Punkty leżą na dwóch sferach (na rysunku − czarne okręgi) Zadanie polega na tym że mając punkty czerwone robię "wirtualny odcinek" (nie ma potrzeby wyznaczania go) Tylko muszę znaleźć odcinek z dwóch punktów niebieskich (leżących na zewnętrznej sferze), który jest najbliższy odcinkowi czerwonemu Dlatego najprościej mi porównywać odległość punktu od punktu, z tym że aby to zadanie było dobrze zrobione muszę wyznaczyć zielone punkty i je mogę porównywać do czerwonych, bo inaczej mogłoby się okazać, że punkty różowe są bliżej niż zielone, a to na wspólnej sferze nie jest prawdziwe.

Peter: Może jeszcze inaczej, Mając dwa niebieskie punkty A(x1,y1,z1) i B(x2,y2,z2) chciałbym wyznaczyć punkt C leżący na wspólnej prostej tych punktów w odległości np. "k" od punktu A w kierunku punktu B. Z tym że potrzebuje mieć współrzędne x,y,z dla punktu C

Adamm: |[A+t(B−A)]−A| = t*|A−B| = k (t>0 żeby leżał w kierunku B) ?

Peter: Teraz to ja za bardzo nie rozumiem... Jak posiadając współrzędne punktu A, wyliczyć współrzędne punktu C przesuniętego o długość wektora V w kierunku punktu B. Czyli 3 punkty leżą na tej samej prostej. Niestety nie znam wartości x,y,z wektora V, mam tylko jego długość całkowitą.

Blee: 1) skoro masz współrzędne A i B to możesz wyznaczyć wzór prostej 2) co więcej − możesz wyznaczyć współrzędne środka tejże sfery (połowa odcinka AB) 3) mniejszy (szukany) odcinek CD będzie zawierał się w odcinku AB, więc będzie leżał na tej samej prostej (wyznaczonej w (1) ) 4) mając współrzędne mniejszej sfery jesteś w stanie wyznaczyć jej wzór ... robisz równanie i otrzymujesz punkty C i D