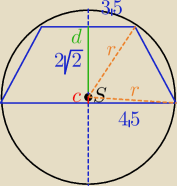
 Podam jeden ze sposobów rozwiązania bez umieszczania tej figury w układzie współrzędnych.
Czy to "po Bożemu", muszę poszukać odpowiedzi [→ kierunek Toruń].
Skorzystam z tego, że trapez wpisany w okrąg jest równoramienny.
c+d=2√2 → d=2√2−c
z tw. Pitagorasa
(3,5)2+d2=r2
(4,5)2+c2=r2
↘
(3,5)2+(2√2−c)2=r2
(4,5)2+c2=r2
i to jest układ równań, z którego obliczam promień okręgu.
Długość promienia wychodzi 4,5, więc środek okręgu należy do dłuższej podstawy trapezu.
Podam jeden ze sposobów rozwiązania bez umieszczania tej figury w układzie współrzędnych.
Czy to "po Bożemu", muszę poszukać odpowiedzi [→ kierunek Toruń].
Skorzystam z tego, że trapez wpisany w okrąg jest równoramienny.
c+d=2√2 → d=2√2−c
z tw. Pitagorasa
(3,5)2+d2=r2
(4,5)2+c2=r2
↘
(3,5)2+(2√2−c)2=r2
(4,5)2+c2=r2
i to jest układ równań, z którego obliczam promień okręgu.
Długość promienia wychodzi 4,5, więc środek okręgu należy do dłuższej podstawy trapezu.
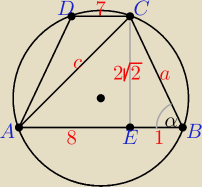 Inny sposób: R − długość promienia okręgu opisanego na trapezie ABCD
i na trójkącie ABC
Inny sposób: R − długość promienia okręgu opisanego na trapezie ABCD
i na trójkącie ABC
| 2√2 | ||
a = √1 + 8 = 3, sinα = | , c = √8 + 64 = 6√2, | |
| 3 |
| c | ||
z tw. sinusów: | = 2R ⇒ R = ... | |
| sinα |