okrąg i koło- geometria zadania
geometria: Cześć, w zadaniach ze zbioru długość okręgu, pole koła nie potrafiłam poradzić sobie w
poniższych zadaniach. Proszę o pomoc.
Te zadania w porównaniu z pozostałymi nie wydają mi się trudne, jednak nie potrafię wpaść na
sposób ich rozwiązania. Nie wiem jak powinnam do nich podejść.
1) Środek każdego z dwóch kół o promieniu r należy do okręgu drugiego koła. Oblicz obwód
figury, która jest sumą tych kół.
ODP: 8/3πr
2) Na wielokącie foremnym opisano okrąg i wpisano weń okrąg. Pole pierścienia zawartego między
tymi dwoma okręgami jest równe π (S). Oblicz długość boku wielokąta.
Z własnych obliczeń doszłam do momentu, gdy wiem, że r=√3/3 (ale nie wiem czy te obliczenia
są poprawne)
ODP: 2 lub inaczej: 2√2/π
3) Trzy koła o jednakowym promieniu r leżą na płaszczyźnie w ten sposób, że środek każdego z
nich leży na okręgach obu pozostałych kół. Oblicz pole figury, która jest częścią wspólną tych
trzech kół.
ODP: π−√3/2 r2
14 wrz 08:59
ite:
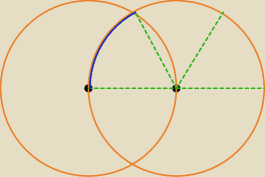
zad.1
Np.Oblicz sumę obwodów obu kół i odejmij cztery długości granatowej krzywej.
14 wrz 09:14
ite: zad. 2
Zrób rysunek jakiegoś wieolokąta np.sześciokąta z wpisanym i opisanym na nim okręgiem.
Znajdź trójkąt prostokątny, którego bokami są promień okręgu wpisanego i promień okręgu
opisanego. Trzecim bokiem Δ będzie połowa boku wielokąta. Skorzystaj z twierdzenia Pitagorasa.
14 wrz 09:29
ite: zad.3
Dobrą podpowiedzią jest rysunek do zad.1 z 9:14
Porównaj pole wycinka koła opartego na niebieskim łuku z polem trójkąta równobocznego o boku
równym promieniowi koła.
14 wrz 09:34
Mila:
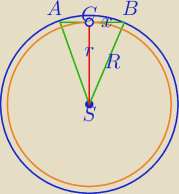
|AB|=2x
1)
P
p=πR
2−πr
2=π*(R
2−r
2)
π*(R
2−r
2)=π⇔R
2−r
2=1, R
2=1+r
2
2) W ΔSCB:
x
2+r
2=R
2
x
2+r
2=1+r
2
x
2=1
x=1
|AB|=2
========
14 wrz 19:23
Eta:
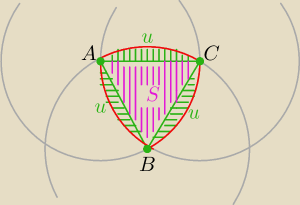
| | r2√3 | |
ΔABC równoboczny o boku długości r i polu S= |
| |
| | 4 | |
pole
u= P(wycinkaACB)−
S
| | 1 | |
P(figury)= 3u+S ⇒ P= |
| πr2−2S=............. |
| | 2 | |
14 wrz 21:04
geometria: Dzięki za wszystkie wskazówki ite, wszystkie zadania udało mi się dokończyć z właściwym
rozwiązaniem

14 wrz 21:17
geometria: Mila, Eta dziękuję

14 wrz 21:17
Eta: 
14 wrz 22:57
 zad.1
Np.Oblicz sumę obwodów obu kół i odejmij cztery długości granatowej krzywej.
zad.1
Np.Oblicz sumę obwodów obu kół i odejmij cztery długości granatowej krzywej.
 |AB|=2x
1)
Pp=πR2−πr2=π*(R2−r2)
π*(R2−r2)=π⇔R2−r2=1, R2=1+r2
2) W ΔSCB:
x2+r2=R2
x2+r2=1+r2
x2=1
x=1
|AB|=2
========
|AB|=2x
1)
Pp=πR2−πr2=π*(R2−r2)
π*(R2−r2)=π⇔R2−r2=1, R2=1+r2
2) W ΔSCB:
x2+r2=R2
x2+r2=1+r2
x2=1
x=1
|AB|=2
========



