zadanka z pól trójkąta Kinga01: Cześć, przerabiam zadanka z geometrii płaszczyzny. Do tych zadań poniżej nie potrafiłam znaleźć odpowiedniego rozwiązania. Proszę o pomoc 1) (330) Dwie wysokości trójkąta równoramiennego mają długość 24 (h), a trzecia 20 (H). Oblicz pole trójkąta. (Odp:300 lub inaczej: (H² h) / √4H² − h² ) 2) (331) Najdłuższy bok trójkąta rozwartokątnego ma długość 60, a wysokości poprowadzone z obu jego końców mają długości 12 i 20. Oblicz pole tego trójkąta. Odp: 225 (√6 − √2) 3) (338) Trójkąt równoramienny o kącie przy podstawie α przecięto prostą przechodzącą przez koniec podstawy i nachyloną do niej pod kątem β (α>β). Wyznacz stosunek pól trójkątów, na jakie prosta podzieliła dany trójkąt. Odp: sin(α−β)/ 2 cosα sinβ

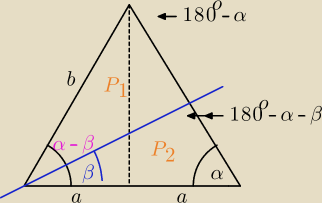ite: zad.3 1/ Skorzystaj ze wzoru na pole trójkąta, gdy znana jest któregoś długość boku i wszystkie kąty tego trójkąta.

	sin(α)*sin(β)
P2=1/2*(2a)2
	sin(180o−α−β)

2/ Zapisz pole P₁ za pomocą tego samego wzoru w odniesieniu do boku b,

	a
3/ Zapisz iloraz pól i skorzystaj z tego że		= cos(α), długości boków się uproszczą.
	b

Kinga01: Dzięki za pomoc! Z 1 zadaniem też już się uporałam.

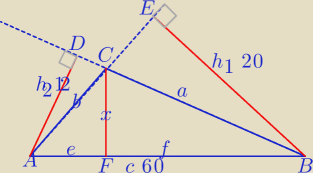Mila: a Zadanie2) 1) 20*b=12*a=60*x b=3x a=5x 2) W ΔAFC: b²=x²+e² ⇔9x⁻x²=e² ⇔8x²=e² e=2√2x 3) W ΔCFB: (5x)²=x²+f² ⇔24x²=f² f=2√6x 4) 2√2x+2√6x=60 /:2 x(√2+√6)=30 *(√6−√2) x*(6−2)=30*(√6−√2)

	15
x=		*(√6−√2)
	2

5)

	1		15
PΔABC=		*60*		*(√6−√2)
	2		2

P_ΔABC=225*(√6−√2) ===================