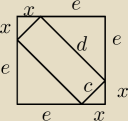
 a − bok kwadratu
e=a−x
Z twierdzenia Pitagorasa:
d2=e2+e2
d2=(a−x)2+(a−x)2
d2=2a2−4ax+2x2
d2=2(a−x)2 ⇒ d=√2(a−x)2
d=√2|a−x|, bo √x2=|x|
d=√2(a−x), bo a>x
Z twierdzenia Pitagorasa:
c2=x2+x2
c2=2x2
c=x√2
Stosunek długości boków prostokąta jest równy 1:4, zatem:
a − bok kwadratu
e=a−x
Z twierdzenia Pitagorasa:
d2=e2+e2
d2=(a−x)2+(a−x)2
d2=2a2−4ax+2x2
d2=2(a−x)2 ⇒ d=√2(a−x)2
d=√2|a−x|, bo √x2=|x|
d=√2(a−x), bo a>x
Z twierdzenia Pitagorasa:
c2=x2+x2
c2=2x2
c=x√2
Stosunek długości boków prostokąta jest równy 1:4, zatem:
| c | 1 | ||
= | |||
| d | 4 |
| c | x√2 | ||
= | |||
| d | √2(a−x) |
| c | x | ||
= | |||
| d | a−x |
| x | 1 | ||
= | |||
| a−x | 4 |
| cd | 2x(a−x) | ||
= | |||
| a2 | (5x)2 |
| cd | 2x*4x | ||
= | |||
| a2 | 25x2 |
| cd | 8x2 | ||
= | |||
| a2 | 25x2 |
| cd | 8 | ||
= | |||
| a2 | 25 |
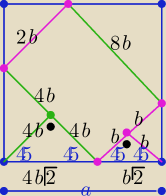 a=5b√2 to P□=50b2
P▭=16b2
a=5b√2 to P□=50b2
P▭=16b2
| P▭ | 16b2 | 8 | |||
= | = | ||||
| P□ | 50b2 | 2 |
 Mógłby ktoś jeszcze poratować jakąś wskazówką do pozostałych zadań?
Mógłby ktoś jeszcze poratować jakąś wskazówką do pozostałych zadań?
 zad.2/ popraw treść.........
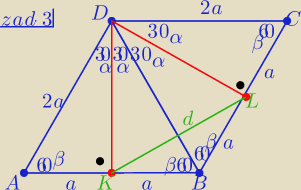
zad3.
1/ rysunek
2/ skoro wysokości są dwusiecznymi to ΔABD i BDC są równoramienne
zatem |AK|=|KB|=a to |AB|=|DC|=2a
3/ w ΔAKD : α+β=90o to 2β=4α ⇒β=2α
to β=60o i α=30o
zatem taki równoległobok jest rombem iskłada się a dwóch trójkątów równobocznych o bokach 2a
4/ z tw. cosinusów wΔBKL
d2=a2+a2−2a*a*cos120o
d2=3a2 ⇒ a2=d2/3
Pole = 4a2*sin60o
zad.2/ popraw treść.........
zad3.
1/ rysunek
2/ skoro wysokości są dwusiecznymi to ΔABD i BDC są równoramienne
zatem |AK|=|KB|=a to |AB|=|DC|=2a
3/ w ΔAKD : α+β=90o to 2β=4α ⇒β=2α
to β=60o i α=30o
zatem taki równoległobok jest rombem iskłada się a dwóch trójkątów równobocznych o bokach 2a
4/ z tw. cosinusów wΔBKL
d2=a2+a2−2a*a*cos120o
d2=3a2 ⇒ a2=d2/3
Pole = 4a2*sin60o
| 2d2√3 | ||
P= | ||
| 3 |
 Wykonaj rysunek to zobaczysz.
Wykonaj rysunek to zobaczysz.

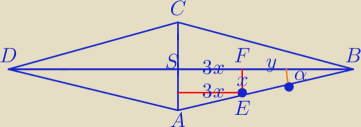 Zadanie 2.
Zadanie 2.
| y | ||||||||
1) W ΔBFE: cosα= | ||||||||
|
| 3x+y | ||
W ΔASB: cosα= | ||
| a |
| y | 3x+y | 2 | |||||||||
= | ⇔y= | (3x+y) | |||||||||
| a | 3 |
| 2 | ||
W ΔBFE: (6x)2+x2=( | a)2 | |
| 3 |
| 4 | ||
37x2= | a2 | |
| 9 |
| 2a | ||
x= | ||
| 3√37 |
| 2a | 6a | |||
|BS|=9* | = | |||
| 3√37 | √37 |
| 6a | ||
|AS|2+( | )2=a2 | |
| √37 |
| 36 | ||
|AS|2=a2− | a2 | |
| 37 |
| a | ||
|AS|= | ||
| √37 |
| 2*6a | ||
4) |AC|= | ||
| √37 |
| 2a | ||
|DB|= | ||
| √37 |
| 12a2 | ||
PABCD= | ||
| 37 |
 dlaczego?
dlaczego?
 Mila
Mila 
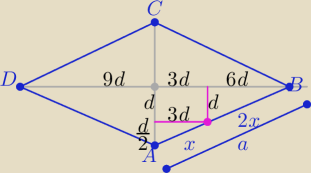 Już widzę,gdzie się "rąbnęłam"
Poprawiam:
Z podobieństwa trójkątów ( oznaczenia długości na rysunku)
|BD|=18d , |AC|=3d to P=27d2
i z tw. Pitagorasa
Już widzę,gdzie się "rąbnęłam"
Poprawiam:
Z podobieństwa trójkątów ( oznaczenia długości na rysunku)
|BD|=18d , |AC|=3d to P=27d2
i z tw. Pitagorasa
| 9 | 4a2 | |||
81d2+ | d2=a2 ⇒ 333d2=4a2 ⇒ d2= | |||
| 4 | 333 |
| 27*4a2 | ||
P= | ||
| 333 |
| 12a2 | ||
P= | ||
| 37 |
