 Wyznacz wartości parametru m, dla których równanie x2−2mx+m2−1 = 0 ma dwa różne pierwiastki,
takie że x1>1 oraz x2 > 1
napisałem takie warunki
1) Δ > 0
2) x1 + x2 >2
3) x1*x2 >1
ale w odpowiedziach jest
1') taki sam
2') xw > 1
3') f(1) > 0
o ile 2 i 2' są tożsamością, to 3 i 3' już nie.
W swoim rozwiązaniu kierowałem się tym, że te pierwiastki muszą być dodatnie i większe od 1
Wyznacz wartości parametru m, dla których równanie x2−2mx+m2−1 = 0 ma dwa różne pierwiastki,
takie że x1>1 oraz x2 > 1
napisałem takie warunki
1) Δ > 0
2) x1 + x2 >2
3) x1*x2 >1
ale w odpowiedziach jest
1') taki sam
2') xw > 1
3') f(1) > 0
o ile 2 i 2' są tożsamością, to 3 i 3' już nie.
W swoim rozwiązaniu kierowałem się tym, że te pierwiastki muszą być dodatnie i większe od 1
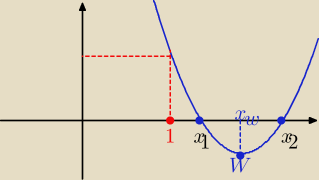 1/Δ>0
i 2/ f(1)>0
i 3/ xw>1
1/Δ>0
i 2/ f(1)>0
i 3/ xw>1

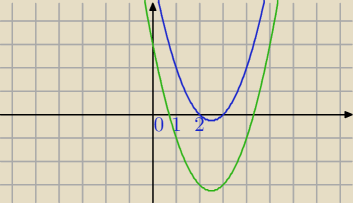 Parabola jest skierowana do góry.
Wykres ma być tego typu co niebieski.
W przypadku wykresu zielonego masz spełniony warunek x1+x2>2 i x1*x2>1 ale x1<1
Dołączony warunek f(1)>0 zapewnia , że obydwa pierwiastki są na prawo od 1.
Parabola jest skierowana do góry.
Wykres ma być tego typu co niebieski.
W przypadku wykresu zielonego masz spełniony warunek x1+x2>2 i x1*x2>1 ale x1<1
Dołączony warunek f(1)>0 zapewnia , że obydwa pierwiastki są na prawo od 1.
| 1 | ||
Przykład: x1= | i x2=3. | |
| 2 |
| 3 | ||
x1x2 = | > 1, | |
| 2 |