trójkąt
michał:
W trójkącie równoramiennym ABC na ramionach AC i BC obrano
odpowiednio punkty E i F tak,że |AE|=|FB| i następnie przez te punkty poprowadzono
proste równoległe do wysokości BD, które przecięły podstawę AC
odpowiednio w punktach P i Q
Wykaż,że |AC|=2|PQ|
8 wrz 19:57
Mila:
AC, BC ramiona , potem masz podstawa AC. Dobrze zapisałeś treść?
8 wrz 20:42
michał:
Bardzo przepraszam
Ma być na bokach AB i BC
Teraz pomożesz?
8 wrz 22:14
Eta:
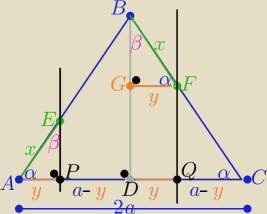
Ten rys. powinien wystarczyć
|AC|=2a
ΔAPE≡ΔGFB z cechy (kbk)
|PQ|=a−y+y ⇒ |PQ|=a
zatem |AC|=2|PQ|
c.n.w.
9 wrz 00:12
 Ten rys. powinien wystarczyć
|AC|=2a
ΔAPE≡ΔGFB z cechy (kbk)
|PQ|=a−y+y ⇒ |PQ|=a
zatem |AC|=2|PQ|
c.n.w.
Ten rys. powinien wystarczyć
|AC|=2a
ΔAPE≡ΔGFB z cechy (kbk)
|PQ|=a−y+y ⇒ |PQ|=a
zatem |AC|=2|PQ|
c.n.w.