trójkąt
maturka:
W trójkąt prostokątny ABC o kącie CAB=300 wpisano okrąg o promieniu √3
Oblicz długość CD, gdzie D jest punktem styczności tego okręgu z przeciwprostokątną AB
7 wrz 22:27
Eta:
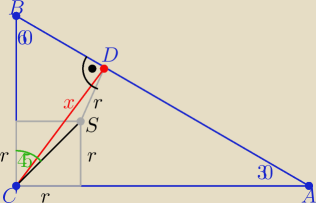
Podaję jeden ze sposobów
|CS|=r
√2 ⇒ |CS|=
√6 , |DS|=r =
√3
w czworokącie BCSD kąt DSC=360
o−(60
o+45
o+90
o) ⇒ |∡DSC|=165
o
| | √2 | |
cos165o=−cos15o = |
| (1+√3) ( wyprowadź sobie ... |
| | 4 | |
z tw. cosinusów w ΔDCS
x
2=6+3+2
√6*
√3*cos15
o
................
x=.....................
a to już dokończ samodzielnie maturzysto
8 wrz 00:07
Mila:
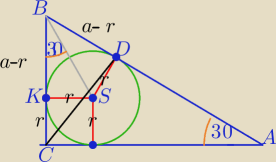
r=
√3, |BC|=a
1) W ΔSKB:
| | r | | √3 | | √3 | |
tg30o= |
| ⇔ |
| = |
| ⇔ |
| | a−r | | 3 | | a−√3 | |
a−
√3=3⇔a=3+
√3
2) W ΔBCD:
|CD|
2=(3+
√3)
2+3
2−2*(3+
√3*3*cos60
o
|CD|=
√12+3√3
===========
sprawdź rachunki
8 wrz 18:26