Określ monotoniczność funkcji Milo:

	x2
Określ monotoniczność funkcji f(x)=
	x−2

Mila: D=R\{2}

	2x*(x−2)−x2*1		x2−4x
f'(x)=		=
	(x−2)2		(x−2)2

f(x)↑ dla x²−4x>0 i x≠2 f(x)↓ dla x²−4x<0 i x≠2 dokończ

Milo: Ja nawet nie wiem co to tu się staneło

PW: Nie wiesz co to jest pochodna?

Jakub: https://www.youtube.com/watch?v=38DRUlDxMqk&feature=share Jeśli pomogłem daj sub i like

Milo: Nope

Mila: 1) Obliczyłam pochodną funkcji. 2) Jeżeli pochodna dodatnia to funkcja jest rosnąca, jeżeli pochodna ujemna to funkcja jest malejąca. Do której klasy chodzisz?

Milo: Nadrabiam zaległości nie byłem dwa lata w Polsce i wróciłem do 2lo to nie istotne

Mila: To zadanie z lekcji?

Milo: Już ogarniam thx

Mila: Dobrze.

Milo: Chociaż jednak nie. Poprosił bym o dalsze rozpisanie jeśli można

Saizou: Twierdzenie Funkcja o pochodnej dodatniej (ujemnej) na przedziale (a; b) jest rosnąca (ujemna).

	x2
f(x)=
	x−2

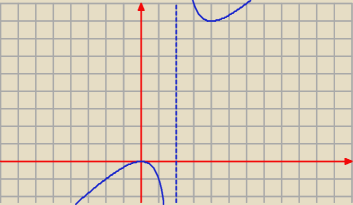
Dziedziną funkcji f jest zbiór R\{2}, ponieważ x−2≠0→x≠2 Obliczamy pochodną funkcji

	(x2)'*(x−2)−x2*(x−2)'
f'(x)=		=
	(x−2)2

2x(x−2)−x2*1
	=
(x−2)2

2x2−4x−x2
	=
(x−2)2

x2−4x
(x−2)2

Dziedziną pochodnej jest zbiór R\{2} Zgodnie z twierdzeniem powyżej mamy,

	x2−4x
f'(x)>0→		>0→x2−4x>0→x(x−4)>0→x∊(−∞; 0)∪(4; +∞)
	(x−2)2

w tym przedziale funkcja rośnie.

	x2−4x
f'(x)<0→		<0→x2−4x<0→x(x−4)<0→x∊(0; 4)
	(x−2)2

ale w dziedzinie nie ma punktu 2, zatem funkcja f jest malejąca w przedziale (0; 4)\{2}

PW: Saizou, tak nie wolno o tym mówić (ostatnie Twoje zdanie jest fałszywe).

Saizou: PW prawda, trochę się zagalopowałem. Powinienem to 2 już wyrzucić na poziomie pochodnej, bo dziedzina funkcji i pochodnej pokrywa się., ewentualnie zbadać co dzieje się w otoczeniu punktu 2

Jerzy: Chyba nadal nie rozumiesz, co PW miał na myśli.

jc: To, że funkcja jest rosnąca na każdym z dwóch rozłącznych zbiorów, nie oznacza, że jest rosnąca na ich sumie.

Jakub: dasdsa