Asymptoty Sempt: Obliczyć dziedzinę i wyznaczyć asymptoty: f(x)=1+ ²_x+⁴_x²+... q=|²_x| <1 ^2−x_x<0 => x należy do (0,2) ⋀ ^2+x_x>0 => x należy do (−∞, − 2) ∪ (0,+∞) zatem D_f=(0, 2) S=^x_x−2 Asymptoty ukośne: y=ax+b a=lim_x→∞ = ^x/(x−2) _x = lim_x→+∞ = ¹_x−2 i jak dalej, ktoś pomoże?

Jerzy: Druga linijka... bzdety.Podstaw sobie x = 1.

Sempt: W takim razie w jaki sposób obliczyć ^2−x_x <0 poprawnie? A co z asymptotami, tam też coś jest źle?

Blee:

	2		2
|		| < 1 <−−−− proponuje narysować f(x) = |		|
	x		x

I gotowe

Blee: albo rozwiązujesz: 1) x > 0

2
	< 1 −> 2 < x
x

2) x < 0

2
	< 1 −> 2 < −x (bo −x>0) −> x < −2
−x

Sempt: Ok, chyba rozumiem zatem z wykresu odczytuję, że D_f= (−∞, − 2) ∪ (2, +∞), zgadza się?

Blee: da

Blee: No i jak już tak bardzo chcesz zaczynać od ukośnej asymptoty to policz granicę do końca ... a zobaczysz, że:

	f(x)
a = lim		= 0
	x

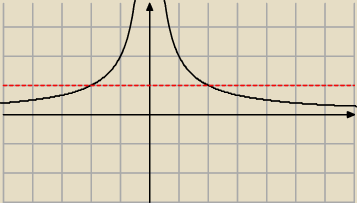
więc: b = lim f(x) = i nasza asymptota ukośna to tak naprawdę asymptota pozioma no i jeszcze patrzymy na asymptotę pionową

Sempt: Czyli b= lim f(x)−ax= ^x_x−2 = [^∞_∞] i teraz z reguły de Hospitala? A jak obliczyć to a=lim ^f(x)_x bo z tym mam właśnie problem...

Blee:

	x		1
serio lim		= lim		=
	x−2		1 − (2/x)

Blee: Sempt −−− to zanim zrobisz to zadanie, to sobie zrób powtórkę z granic, bo takie granice to powinieneś w pamięci rozwiązywać, z zawiązanymi oczami i to po pijaku

Blee:

	1
do czego dąży		czy to dla x−> +∞ czy to dla x−> −∞
	x−2

Sempt: Do +∞ na razie b=lim_+∞ =¹_1−(2/x) = ¹₁₋₀ = 1?

Blee: no i do −∞

Sempt: Dla − ∞ to samo? Nie wiem, bo dalej nie ogarniam jak policzyć a=lim ¹_x−2

Blee: tak ... będzie to samo dla +∞

1		1		1
	−>		=		−> 0
x−2		∞ − 2		∞

dla −∞

1		1		1
	−>		= −		−> 0
x−2		−∞ − 2		∞

Blee: Jeszcze raz napiszę −−− wróć do PODSTAW związanych z granicami

Jakub: https://m.youtube.com/watch?v=n7eRk8r8L2o

Sempt: Dzięki