Prawdopodobieństwo, że losowo wybrany punkt zbioru należy do okręgu Mateusz: Prawdopodobieństwo, że losowo wybrany punkt zbioru należy do okręgu wynosi? Zbiór: { (x,y) ∊ R² : 2 < | x | < 4, 2 < | y | < 4} Okrąg: { (x,y) ∊ R² : (x+2)² + (y−2)² = 4}

Mila: Czy nie powinno być: ....wybrany punkt zbioru należy do wnętrza okręgu? Jeśli to test wyboru , to podaj jakie są odpowiedzi?

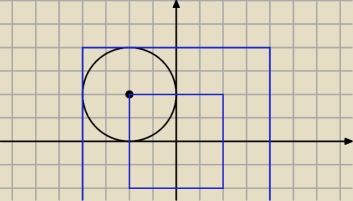
Blee: przestrzeń zdarzeń to niebieska ramka, a więc #Ω = 8² − 4² = 64 − 16 = 48

	3
Pole obszaru okręgu w tej ramce to: #A =		π22 = 3π
	4

	3π		π
P(A) =		=
	48		16

Mila: Wg mnie to inny jest obszar niebieski − 4 kwadraciki. Jeden wspólny z kołem −lewy górny. Może JC popatrzy?

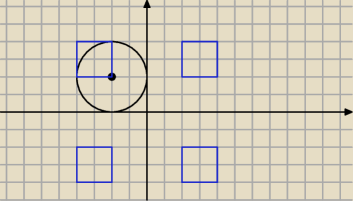
Blee: faktycznie pośpieszyłem się taki winien być obszar

Mila:

Mateusz: Dziękuje za odpowiedzi! @Mila Odpowiedzi są takie: a) π/16 b) π/48 c) 1 − π/16 d) 0 Czyli zgodnie z obliczeniami @Blee, odpowiedź A

Mila:

	0.25π*22		π
P(A)=		=		wg rys.21:36
	4*22		16