Prostokąt cx: Dany jest prostokąt ABCD, w którym |AB| : |AD| = √2. Punkt S jest środkiem boku AB. Oblicz miare kąta między prostymi AC i DS.

Mila: https://zadania.info/d166/9020985

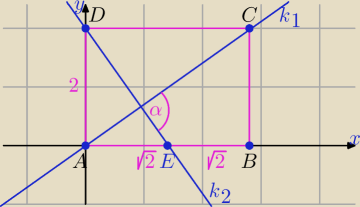
Bogdan: Proponuję takie rozwiązanie: Przyjmuję: |AD| = 2, |AB| = 2√2 A = (0, 0), B = (2√2, 0), C = (2√2, 2), D = (0, 2), E = (√2, 0)

	2 − 0		1
prosta k1: y = a1x + b1, a1 =		=
	2√2 − 0		√2

	2 − 0
prosta k2: y = a2x + b2, a2 =		= −√2
	0 − √2

a₁*a₂ = −1 ⇒ k₁⊥k₂ i α = 90^o

Mila:

a
	=√2 ⇔a=b√2
b

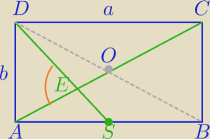
1) AO i DS− środkowe w ΔDAB |AC|=d d²=a²+b²=3b² ⇔d=b√3

	1		b√3
|AE|=		d=
	3		3

	2
|DE|=		|DS|
	3

	b√2
|DS|2=b2+(		)2
	2

	3		√6
|DS|2=		b2 ⇔|DS|=		b
	2		2

|DE|=U{√6b}}{3} 2) W ΔAED:

	b√3		√6b		√3b		√6b
b2=(		)2+(		)2−2*		*		*cos∡E /:b2
	3		3		3		3

	3		6		2√12
1=		+		−		*cosE
	9		9		9

cosE=0⇔|∡AED|=90^o =================

Bogdan: Dziękuję sam sobie, dziekuję Mili, bo cx nie zna takiego słowa

Blee: Dostał gotowca ... dostał ... więc za co ma dziękować? To w sumie MY powinniśmy mu dziękować, że przyszedł i wspaniałomyślnie wrzucił zadanie ... gdyby nie on, to nie wiem co byśmy wtedy robili, pewnie dłubali w nosie

Mila: Teraz tak jest. Pozdrawiam Panów. Będzie lepiej