Dwusieczne w prostokącie
Ania:
1)
W prostokącie ABCD , w którym stosunek długości boków AB i BC jest równy 8:6,
poprowadzono dwusieczne kątów ADB i BDC .
Dwusieczne te przecinają boki AB i CB odpowiednio w punktach K i M .
Oblicz stosunek pola prostokąta ABCD do pola trójkąta DKM .
24 sie 21:31
Eta:
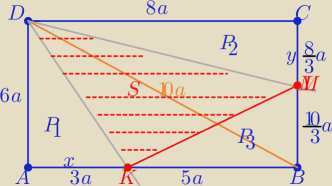
|BD|=
√(8a)2+(6a)2 ⇒ |BD|=10
|AK|=x to |KB|=8a−x i |CL|=y to |BM|=6a−y
Z tw. o dwusiecznej
w ΔADB i w Δ BDC
| 10a | | 8a−x | | 10a | | 6a−y | |
| = |
| i |
| = |
| |
| 6a | | x | | 8a | | y | |
...................................
| | 8 | | 10 | |
to |AK|=3a , |KB|=5a , |CM|= |
| a , |BM|= |
| a |
| | 3 | | 3 | |
P(ABCD)=48a
2
S(DKM)= P−P
1−P
2−P
3
...........................
S=................
dokończ
24 sie 22:19
Mila :
To najprostszy sposób

24 sie 22:46
Mila:
24 sie 22:47
 |BD|=√(8a)2+(6a)2 ⇒ |BD|=10
|AK|=x to |KB|=8a−x i |CL|=y to |BM|=6a−y
Z tw. o dwusiecznej
w ΔADB i w Δ BDC
|BD|=√(8a)2+(6a)2 ⇒ |BD|=10
|AK|=x to |KB|=8a−x i |CL|=y to |BM|=6a−y
Z tw. o dwusiecznej
w ΔADB i w Δ BDC
