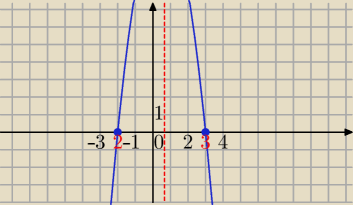
Funkcja kwadratowa Sandra: Dana jest funkcja kwadratowa w postaci iloczynowej f(x)= −2(x−3) (x+2), x nalezy do liczb rzeczywistych. a)Napisz wzor funkcij f w postaci kanonicznej oraz ogólnej. b)Naszkicuj wykres funkcji f c)Określ zbior wartosci funkcji f, przedzialy monotoniczności oraz zbior tych argumentów, dla których funkcjia f przyjmuje wartości niedodatnie.

Jerzy: matematyka.pisz.pl/forum/391362.html

Mila: Napisz dobrze wzór funkcji kwadratowej.

ICSP: f(x) = −2(x−3)(x+2) , x ∊ R Jest napisany poprawnie tylko wkradł się niepotrzebny enter.

Mila: f(x) = −2(x−3)(x+2) , x ∊ R 1) x₁=−2, x₂=3 Współrzędne wierzchołka paraboli:

	−2+3		1
p=xw=		=
	2		2

	1		1		5		5		25
q=yw=−2*(		−3)*(		+2)=−2*(−		)*		=		=1212
	2		2		2		2		2

Postać kanoniczna: f(x)=a*(x−p)²+q

	1		1
f(x)=−2*(x−		)2+12
	2		2

=================== Postać ogólna : y=−2*(x²+2x−3x−6)=−2(x²−x−6) f(x)=−2x²+2x+12 ============ Z tej postaci też możesz wyznaczyć wsp. wierzchołka paraboli;

	−b		−2		1
xw=		=		=
	2a		−4		2

	1		1		1		1
yw=f(		)=−2*		+2*		+12=−		+1+12=1212
	2		4		2		2

Postać kanoniczna j,w ================

	1
2)Zwf=(−∞,>12		> − zbiór wartości funkcji:
	2

=============== x=U{1}[2}− oś symetrii paraboli f(x)↑ dla x∊(−∞,{1}{2}>

	1
f(x)↓ dla x∊<		, ∞) Podałam maksymalne przedziały monotoniczności.
	2

3) f(x)≤0 dla x∊(−∞,−2>∪<3, ∞) wartości niedodatnie funkcji f(x) ================================= f(x)>0 dla x∊(−2,3) wartości dodatnie f(x)

PNM:

BAI PING TING: