stereometria stereometria_to_zło: Trójkąt równoboczny o obwodzie 12 cm obraca się dookoła prostej przechodzącej przez jego wierzchołek i równoległej do przeciwległego boku. Oblicz objętość i pole powierzchni otrzymanej bryły.

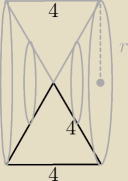
Blee: w efekcie otrzymujesz bryłę którą można opisać jako: walec o promieniu podstawy r i wysokości h = 4

	4
wyciętymi dwoma stożkami o promieniu podstawy r i wysokości h1 =		= 2
	2

Blee: związku z tym V będziesz liczyć ze wzoru:

	1		h
V = πr2h −		πr2*		(wyznacz r i gotowe)
	3		2

Pole powierzchni całkowitej to już trochę więcej zabawy. Można np. w taki sposób: A −−− pole powierzchni całkowitej walca B −−− pole powierzchni całkowitej JEDNEGO stożka P_c = P_A + 2*P_B − 4*πr² Można też po prostu liczyć powierzchnie boczne walca i stożków

stereometria_to_zło:

	1		h
Czy we wzorze na objętość nie powinno być V=πr2h− 2*		πr2*		?
	3		2

stereometria_to_zło: Obliczyłam P jako pole boczne walca odjąć 2x pole boczne stożka. Wyszło mi 8 √3 π.

stereometria_to_zło: Jednak coś pomieszałam. Pole mi wyszło 32 √3π.

Blee: winno być

Blee: a czemu ODJĄŁEŚ pole boczne stożka

stereometria_to_zło: No właśnie nie wiem, haha, ale już naprawione. Wyszło mi 32√3π

stereometria_to_zło: Nie mam odpowiedzi, ale myślę, że już dobrze. Bardzo dziękuję za pomoc!

Blee: A jaki r czy wyszedł Bo patrząc na Twoje liczby to:

	5
Pboczne walca = 20√3π −> Obpodstawy = 5√3π −> r =		√3
	2

Tak Ci wyszło (Mam nadzieję, że nie)

Blee: no dobra ... dobrze policzyłeś −−− po prostu to 8√3π to nie było odjęcie P_b dwóch stożków tylko jednego

stereo: P_c= P_b (walca)+2P_b(stożka)