liczby zespolone, wyznacz zbiór liczb zpełniających warunek
TiReX: wyznacz i zaznacz na płaszczyźnie zbiór wszystkich z spełniających warunek:
|z|+|z−2j|=2, gdzie z to liczba zespolona
14 sie 17:24
Adamm:
14 sie 18:37
Adamm:
równość w nierówności Minkowskiego
z = 2j−λz, λ≥0 lub z = 0
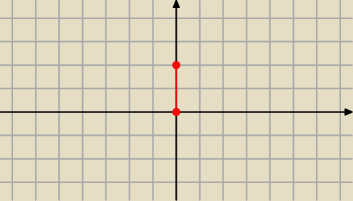
z = tj, t∊[0, 2]
14 sie 18:41
TiReX: Ale w takim razie jak z przykładem |z+j|+|z−j|=4 , odległość tego odcinka nie będzie równa 4
przecież tylko 2 ?
Albo jak by był jakiś przykład gdzie by było odejmowanie między modułami? |z−j|−|z+j|=4 ?
14 sie 21:45
PW: |z+j| to odległość punktu z = (x, y) od punktu −j= (0, −1).
|z−j| to odległość od punktu (x, y) do punktu (0, 1).
Suma tych odległości jest stała (równa 4).
Rysowanie elipsy "metodą ogrodnika".
14 sie 21:55
Mila:
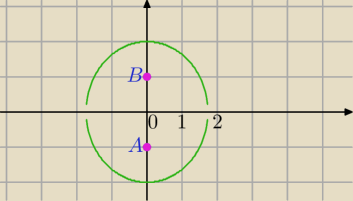
|z+j|+|z−j|=4 − elipsa
A=(0,−1), B=(0,1)− ogniska
|AB|=2 − odległość ogniskowa
2c=2, c=1
2b=4, b=2
c
2=b
2−a
2
1=4−a
2, a
2=3
zbiór punktów płaszczyzny− elipsa.
II sposób
z=x+iy, gdzie x,y ∊R
√x2+(y+1)2+
√(x2+(y−1)2=4
14 sie 22:18
TiReX: To ja już nie bardzo rozumiem, czy elipsa, czy odcinek, można by bardziej łopatologicznie, jak
dla debila, bardzo proszę?
15 sie 01:43
Mila:
W przypadku sumy modułów ( liczby zespolone):
1) W pierwszym przypadku:
|z|+|z−2j|=
2
A=(0,0), B=(0,2) ( rysunek
Adamma
|AB|=2=
2
Równanie opisuje zbiór punktów P(x,y) takich , że suma odległości |AP|+|PB|=2⇔|AB|=2
− szukanym zbiorem jest odcinek AB
( Jeżeli P leżałby poza tym odcinkiem, to z nierówności Δ : |AP|+|PB|>2 )
2)
|z+j|+|z−j|=
4
|AB|=2 <
4 −elipsa ( przypomnij sobie definicję elipsy)
Równanie opisuje zbiór punktów P(x,y) , takich że |AP|+|BP|=
4
√x2+(y+1)2+
√x2+(y−1)2=4
√x2+(y+1)2=4−
√x2+(y−1)2 /
2
x
2+y
2+2y+1=16−8
√x2+(y−1)2+x
2+y
2−2y+1
2y=16−2y−8
√x2+y2−2y+1
4−y=2
√x2+y2−2y+1 /
2 ( y<4)
16−8y+y
2=4(x
2+y
2−2y+1)
16−8y+y
2=4x
2+4y
2−8y+4
4x
2+3y
2=12 /:12
| x2 | | y2 | |
| + |
| =1 równanie elipsy |
| 3 | | 4 | |
=========================
15 sie 21:31
Adamm:
|z|+|2j−z| = |z+(2j−z)|
nierówność trójkąta to specjalny przypadek nierówności Minkowskiego
skorzystałem z tego, że równość w nierówności Minkowskiego zachodzi
wtedy i tylko wtedy gdy wektory są liniowo zależne z nieujemnym parametrem
i. e.
|z1|+|z2| = |z1+z2|
wtedy i tylko wtedy gdy
z2 = λz1 lub z1 = 0 gdzie λ≥0
15 sie 21:39

 |z+j|+|z−j|=4 − elipsa
A=(0,−1), B=(0,1)− ogniska
|AB|=2 − odległość ogniskowa
2c=2, c=1
2b=4, b=2
c2=b2−a2
1=4−a2, a2=3
|z+j|+|z−j|=4 − elipsa
A=(0,−1), B=(0,1)− ogniska
|AB|=2 − odległość ogniskowa
2c=2, c=1
2b=4, b=2
c2=b2−a2
1=4−a2, a2=3