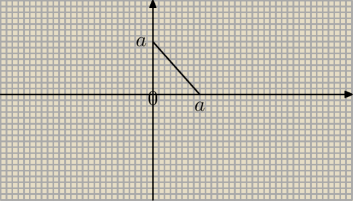
obszar Tymon: Obliczyć całkę _D∫∫sinxcosy dxdy na obszarze trójkąta o bokach w punktach A(0,0), B(a,0), C(0,a) zatem y = −ax + a z tego wynika więc, że −ax+a ≤ y ≤ a oraz 0 ≤ x ≤ a czy przedziały są dobrze wyznaczone?

ABC: nie są dobrze wyznaczone

Tymon: a jakaś podpowiedź?

ABC: po pierwsze odcinek łączący punkty (0,a) i (a,0) nie jest zawarty w prostej y=−ax+a , podstaw sobie np a=3 po drugie wiesz jak się liczy całkę po obszarze który jest normalny względem którejś z osi układu?

Tymon: racja, funkcja to y = −x + a i jest to oczywiście obszar normalny względem osi oy? y = −x + a x = −y + a czy dobrze myślę?

Tymon: a potem −y+a ≤ x ≤ y 0 ≤ y ≤ a

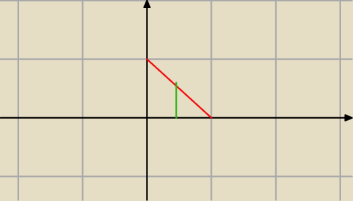
ABC: niech x zmienia się od 0 do a dla ustalonego x, jak zmienia się y ? (zielony pasek) idę spać

Tymon: od −x + a do a?

Adamm: 0≤y≤a(1−x), 0≤x≤1

ABC: ja proponuję 0≤x≤a 0≤y≤a−x

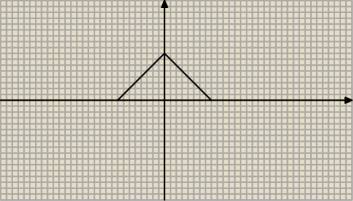
Tymon: dobrze, chyba rozumiem co i jak. D∫∫(2x+1)dxdy na obszarze trójkąta A(−1,1), B(1,1), C(0,0) −1≤x≤1 0≤y≤x ?

Tymon:

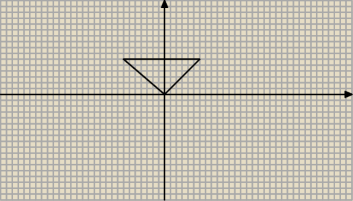
Tymon: a raczej odwrotnie

ABC: możesz na przykład tak y zmienia się od 0 do 1 dla ustalonego y , x zmienia się od ... do ... ?

Mariusz: od −y do y

Tymon: okej dobra doszedłem do tego wyniku bez zaglądania na forum: już ostatnie, miejmy nadzieje, że weszło mi do głowy: punkty (0,0),(2,2)(−1,1) obszar to będzie x od −1 do 2 y od 0 do 1/3x + 4/3? albo jesli normlany względem osi oy y od o do 2 x od −y do 3y+4