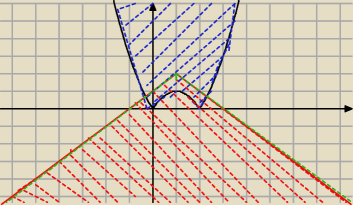
Uklady BAI PING TING: Zadanie nr 3 Wyznacz wszystkie pary liczb calkowitych spelniajacych uklad nierownosci {y−|x²−2x|≥0 {y+|x−1|≤2 zadanie rozwiaz dwoma sposobami y≥|x²−2x| y≤2−|x−1| Zrobilem wykresy tych fucji i zanaczylem obszary tych nierownosci A jak to rozwiazac algebraicznie ?

Adamm: naprawdę sądzisz że algebra powie ci coś więcej niż po prostu |x²−2x|≤y≤2−|x−1| ?

Adamm: aa, całkowitych

BAI PING TING: Linie tych krzywych tez wchodza do rozwiazania Rozwiazanie to czesc wspolna

Mila: cd. zapisu Adamma y≥0 i y≤−|x−1|+2 0≤−|x−1|+2 |x−1|≤2 −2≤x−1≤2 /+1 −1≤x≤3 Sprawdzamy kolejno nierówność: |x²−2x|≤y≤2−|x−1| 1) x=−1 |1+2|≤y≤2−2 F 2) x=0 0≤y≤1 (0,0), (0,1) 3) x=1 |1−2|≤y≤2−|1−1| 1≤y≤2 (1,1),(1,2) Dalej sam

BAI PING TING: Witam Moze najpierw mi wytlumacz dlaczego Adamm zastosowal taki zapis nierownosci i swoj zapis do Sprawdzamy kolejno nierownoswc W odpowiedzi mam wypisane 6 takich par i jest wskazowka zeby rozpatrzyc 4 przypadki x∊(−∞0) x∊<0,1) x∊<1,2) x∊<2,∞)

Nowy: Jeśli y ≥ A i y ≤ B , to znaczy: A ≤ y ≤ B

Mila: Adamm zapisał układ nierówności w inny sposób. np. a≥2 i a≤6 możesz zapisać: 2≤a≤6 Różnie można rozwiązywać, moim sposobem też będzie 6 par.

BAI PING TING: To zrozumialem Teraz wytlumacz mi prosze jaki bylby zapis gdyby obie nierownosci mialy zwrot ≤ lub ≥?

BAI PING TING: takze Mila twoj zapis do tego momentu co napisalem (moze go zalapie Potem sprobuje rozwiazac

BAI PING TING: No to moze inaczej to zrobmy x²−2x ≥0 dla x∊(−∞,0> U<2,∞) tutaj |x²−2x|= x²−2x x²−2x<0 dla x∊(0,2) tutaj |x²−2x|= −x²+2x = 2x−x² x−1≥0 to x≥1 wiec x∊<1,∞) tutaj |x−1|= x−1 x−1<0 to x<1 wiec x∊(−∞,1) tutaj |x−1|= −x+1= 1−x Prosze abys pokazala mi jak zaczac to liczyc dla x∊(−∞,0) sposobem z ewskazowki

BAI PING TING: Potem wroce do Twojego zapisu . Tak nawiasem mowiaz chyba za zbyt ambitne zadania sie wzialem

Jerzy: Chyba kolego nie rozumiesz,że rozwiązujesz to zadanie w zbiorze liczb całkowitych. Czytaj uważnie,co napisała Mila 18:43

BAI PING TING: Jerzy Jasne ze nie rozumiem .Dlatego dopytuje Chce najpierw zrobic to zadanie zgodnie ze wskazowka w zbiorze zadan Ok? Jesli bym je zrobil do dostalbym ocene celujaca na maturze .

Mila: y − I x² −2x I ≥ 0 y + I x −1 I ≤ 2 /*(−1) y − I x² −2x I ≥ 0 −y−|x−1|+2≥0 =========== + −|x²−2x|−|x−1|+2≥0 |x²−2x|+|x−1|−2≤0 Teraz w przedziałach : Otrzymasz całkowite : x∊{0,1,2} i sprawdzasz jak pokazałam.

BAI PING TING: Doszedlem juz Mila do rozwiazania Ogladam na internecie rumuski Mam talent i znalazlem taka perelke https://www.youtube.com/watch?v=Ml4l6SXOc_k

BAI PING TING: xiexieMilu −dziekuje Ci Milu

Mila: To pięknie Dobranoc

BAI PING TING: Dobrej nocy