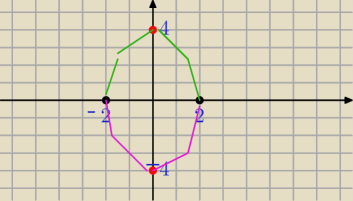
Wykres funkcji BAI PING TING: Mam pytanie czy tak bedzie wygladal wykres |y|=−x²+4?

Mila: https://www.wolframalpha.com/input/?i=%7Cy%7C%3D-x%5E2%2B4

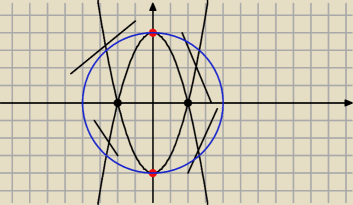
BAI PING TING: Zadanie mam takie A) Rozwiaz graficznie i algebraicznie uklad rownan { |y|= −x²+4 {x²+y²=16 B) Wyznacz wszystkie wartosci parametru a dla ktorych uklad {y=ax²+4 {x²+y²=16 A) Mysle ze bedzie to tak |y|= −x²+4 ⇔y=−x²+4 dla y≥0 lub y=x²−4 dla y<0 Drugie rownanie przedstawia brzeg kola o srodku w punkcie (0,0) i promieniu r=4 Algebraicznie |y|²= y² Podstawiam do drugiego rownania x²+(−x⁺4)²=16 x²+x²−8x+16=16 2x²−8x=0 /(:2) x²−4x=0⇒x=0 lub x=4 Dla x=0 |y|= 4 to y=4 lub y=−4 tutaj by mi sie zgadzalo z wykresem x=4 |y|=−4²+4=−12 odpada Czy podpunkt A) dobrze ?

ite: |y|= −x²+4 ⇒ −2≤x≤2 dlaczego po podstawieniu do drugiego równania otrzymujesz x²+(−x+4)²=16 a nie x²+(−x²+4)²=16

Mila: Oj, Ite ma rację, popatrzyłam tylko na wynik

BAI PING TING: ite Dlatego ze spaprany zapis z tym plusikiem na gorze Jutro juz to poprawie dziekuje za zwrocenie uwagi

BAI PING TING: W podzięce za zwrócenie uwagi https://www.youtube.com/watch?v=30ofpehbp64&list=RD30ofpehbp64&index=1

ite: ¡gracias!

BAI PING TING: No to na dobranoc jeszcze do poduszki https://www.youtube.com/watch?v=USK1VjV-nO8&list=RD30ofpehbp64&index=22

BAI PING TING: Poprawiam zly zapis |y|=−x²+4 Dlaczego nalezy przyjac zalozenie ze −2≤x≤2? To jedno pytanie Pytanie drugie wobec tego czy zamiast tego pierszego zalozenia moge sobie przyjac zalozenie ze −4≤y≤4?. Czy nalezy rozpatrywac lacznie te zalozenia ? Prosze najpierw o odpowidzi na te moje pytania Potem zaczne rozwiazywac dalej

Nowy: Musi być: − x² + 4 ≥ 0 ⇔ x² ≤ 4 ⇔ x ∊ <−2;2>

Nowy: Odpowiedz sobie na pytanie, skąd taki warunek.

Nowy: Co do y , nie robisz żadnych założeń.

BAI PING TING: |y|=−x²+4 |y|²= y² x²+(−x²+4)²=16 x²+x⁴−8x²+16=16 x⁴−7x²=0 x²(x²−7)=0 x=0 lub x=√7 lub x=−√7 i na tym sie na razie zatrzymam Poczekam na odpowiedzi na moje pytania wyzej

BAI PING TING: Wiec tak Pewnie chodzi o to ze wartosc bezwzgledna jest zawsze nieujemna .tak ?

Nowy: Dokładnie.

BAI PING TING: Dziekuje Ci . Wiec zostaje nam tylko rozwiazanie x=0 Wynik mam juz w poscie wyzej

BAI PING TING: Podpunkt B) x²+(ax²+4)²=16 x²+a²x⁴+8ax²+16=16 x²+a²x⁴+8ax²=0 x²(a²x²+8a+1)=0 To rownanie mam miec jedno rozwiaznie Nie potrafie tego dokonczyc

Nowy: Jedno już widać,czyli nawias musi nie mieć rozwiązań lub jedno równe zero.

BAI PING TING: Juz dokoncze . dzieki za pomoc

BAI PING TING: Mam rownanie x²(a²x²+8a+1)=0 ⇔x²=0 ⇒x=0 lub a²x²+8a+1=0 Jednak tutaj czegos nie rozumiem Skoro przyjmuje ze x=0 to niezaleznie od wartosci a cale to rownanie jest spelnione Wiec dlaczego w odpowiedzi jest a∊<−0,125 ,∞)?

Jerzy: Napisałem Ci wyrażnie 13:05.

	−8a − 1
a2x2 + 8a + 1 = 0 ⇔ x2 =
	a2

	−8a − 1
Teraz musi być:		≤ 0 bo wtedy nawias ma jedyne rozwiązanie x = 0 , gdyż : x2
	a2

musi być nieujemny

	1
−8a − 1 ≤ 0 ⇔ a ≥ −		⇔ a ≥ −0,125
	8

ABC: warunkiem na to co napisano o 13:05 jest 8a+1≥0

	1
8a+1≥0 ⇔ 8a≥−1 ⇔ a≥−
	8

BAI PING TING: Szy (tzn tak)