wd tryg: 501. dla jakich wartości parametru m równanie sin2x+sinx+m=0 ma rozwiązania

Kama: Ja bym zrobiła tak: sin2x = 2sinx*cosx 2sinx*cosx + sinx + m = 0 cosx wyznaczyć jedynki trygonometrycznej i podstawić, następnie podstawienie sinx = t i powstaje równanie kwadratowe, z którego delta powinna być większa bądź równa 0 by były rozwiązania.

tryg: tam miało być sin²x+sinx+m=0 więc od razu mamy równanie kwadratowe, rzecz w tym, że sam warunek na deltę to za mało. Dodatkowo pierwiastek/tki mają leżeć w przedziale <−1,1> i tego już nie umiem ując w warunkach... próbowałam z x_w∊<−1,1> i f(−1)≥0 i f(1)≥0, ale niedokońca mam poprawny wynik, więc chyba trzeba trochę inaczej. tylko jak?

tryg:

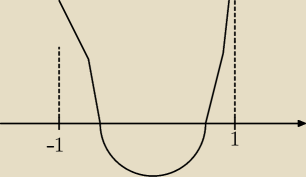
Godzio: f(−1) ≥ 0 f(1) ≥0 sinx = t t² + t + m =0 Δ>0

	1
m<
	4

f(−1) = 1 −1 + m ≥0 m≥0 f(1) = 1+1+ m = 2+m ≥ 0 m≥−2

	1
m∊<0,		)
	4

chyba tak powinno być