potrzebna za zaraz michal cynarski: Znajdź najmniejszą wartość ułamka x⁴+x²+5/(x²+1)²

Adamm: https://www.wolframalpha.com/input/?i=x%5E4%2Bx%5E2%2B5%2F(x%5E2%2B1)%5E2+minimize

michal cynarski: ale skąd sie to wzięło

Mila:

	x4+x2+5
f(x)=
	(x2+1)2

Taki zapis ?

michal cynarski: Tak

Adamm: w takim razie to proste

	1		5
f(x) = 1−		+
	1+x2		(x2+1)2

funkcja kwadratowa z u = 1/(1+x²)

Takie Tam: Podstaw u = x²+1. x∊R ⇒ u∊[1,+∞)

	(u−1)2 + (u−1) + 5		u2−u+5		1		5
f(x(u)) =		=		= 1 −		+
	u2		u2		u		u2

Teraz z pochodnej

df		1		10
	=		−		= 0 ⇔ u = 10 ⇒ fmin = 1 − 0.1 + 0.05 = 0.95
du		u2		u3

Mila:

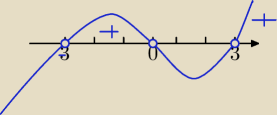
	x4+x2+5		x4+2x2+1−x2+4
f(x)=		=
	x4+2x2+1		x4+2x2+1

	−x2+4		−x2+4
f(x)=1+		=1+
	(x4+2x2+1		(x2+1)2

	−2x*(x2+1)2−(−x2+4)*2*(x2+1)*2x
f'(x)=
	(x2+1)4

f'(x)=0⇔ −2x*(x²+1)²−4x*(−x²+4)*(x²+1)=0 (x²+1)*[−2x*(x²+1)−4x*(−x²+4)]=0⇔ −2x³−2x+4x³−16x=0 2x³−18x=0 2x*(x²−9)=0 x=0 lub x=3 lub x=−3 x*(x−3)*(x+3)>0 x=0 − maksimum lokalne, f(0)=5

	95		19
x=3− minimum lokalne, f(3)=f(−3)=		=
	100		20

x=−3− minimum lokalne lim _x→±∞f(x)=1

	19
Zwf=<		,5>
	20

	19
Najmniejsza wartość f(x) jest równa		.
	20

michal cynarski: dzięki