zaznacz zbiory na rysunku
ite:
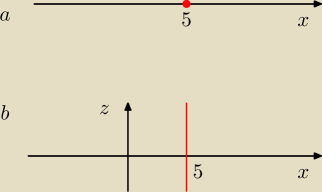
Mam na rysunku zaznaczyć zbiory:
a/ {x∊ℛ | ∀x∃x(x=5)} to ta czerwona kropka na osi
b/ {z∊ℛ | ∀x∃x(x=5)} i tu zupełnie nie wiem ? ? ?
2 sie 09:20
Adamm:
coś nie halo
dla każdego x istnieje x?
2 sie 12:27
ite: No tak, błąd. Muszę się trochę nad tym zastanowić.
2 sie 15:06
wredulus_pospolitus:
a co to jest
z∊R
(a) tu jesteś w R
1 i masz dobrze
(b) tutaj jesteś w R
2, więc zbiór masz {(x,y)∊R
2 | x=5}
2 sie 16:24
ite:
Mój rysunek a) może być ilustracją zbioru {x∊ℛ | ∃x(x=5)}, ale czy {x∊ℛ | ∀x∃x(x=5)} też?
wredulus to zadanie ma dwa kolejne podpunkty, które też nie wiem, jak ruszyć:
jeden taki, jak zapisałam: {z∊ℛ | ∀x∃x(x=5)}
i drugi {z∊ℛ | ∃x∀x(x=5)} ← nie wpisałam go, bo liczyłam, że jak zrozumiem ten poprzedni, to
ten narysuję bez pomocy. Nigdzie nie ma mowy o R2, więc mój rysunek pewnie też jest zły.
3 sie 19:36
Adamm:
Co to niby znaczy ∀x skoro x jest ustalone?
@wredulus chyba wie, skoro się tak wypowiada
3 sie 19:43
4 sie 01:01
Adamm:
I... powiedzieli dokładnie to samo. Nie ma to większego sensu.
4 sie 01:18
ite:
Czy zbiór wyznaczony przez warunek z 18:43 w tym linku,
| | 1 | |
czyli {x∊ℛ | ∃y(y<x ∧ x≤y+ |
| ∧ y≥1)} to x∊(1;1,5> ? |
| | 2 | |
4 sie 17:33
Adamm: a np. 2?
4 sie 19:10
Adamm:
Ten zbiór to po prostu (1, ∞)
4 sie 19:10
ite: Widzę błąd, dziękuję.
4 sie 20:43
ite: W tym zadaniu jest jeszcze jeden podpunkt, nieomówiony w podanym linku.
{<x,y>∊ℛxℛ | ∀z(y2+(x−z)2≠1) ⇒ ∃z((x−z)2+(y−z2)2=1)}
Korzystam z podpowiedzi (p⇒q)⇔((¬p)∨q), zamieniam na
{<x,y>∊ℛxℛ | ∃z(y2+(x−z)2=1) ∨ ∃z((x−z)2+(y−z2)2=1)}.
Czy warunek ∃z(y2+(x−z)2=1) spełniają pary: x dowolne a −1<y<1 ?
4 sie 21:24
Adamm:
−1≤y≤1, tak
4 sie 21:53
ite:
Dla ∃z((x−z)2+(y−z2)2=1) pary: x dowolne y≥−1 jest poprawną odpowiedzią?
5 sie 08:15
Adamm:
nie, ale nie wiem jak to lepiej zapisać
8 sie 19:44
ite:
Czyli ten ostatni warunek ∃z((x−z)2+(y−z2)2=1), to nie będzie półpłaszczyzna wyznaczona
przez prostą y=−1.
A jakie pary go spełniają, bo zupełnie nie wiem ?
8 sie 22:25
Adamm:
to będzie suma okręgów o środkach (z, z2)
inaczej mówiąc
będą to punkty których odległość od paraboli (z, z2) jest ≤ 1
8 sie 23:48
Adamm:
czyli całość to zbiór punktów (x, y), y≤1, oddalonych od paraboli (z, z2) o co najwyżej 1
8 sie 23:51
Adamm:
teraz dopiero zauważyłem że to ma bardzo przyjemną interpretację geometryczną
8 sie 23:53
ite:
Dziękuję za odpowiedź, widzę okrąg, który przejeżdża po paraboli o wierzchołku (0,0) i
ramionach skierowanych w górę.
Ale pytam dalej : )
Dlaczego otrzymany zbiór punktów (x, y) nie będzie taki że y≥−1 zamiast y≤1 (23:51) ?
To będzie ten sam zbiór jak dla warunku ∃z((x−z)2+(y−z2)2≤1), tak ?
9 sie 09:01
Adamm:
bo y≥−1 jest zawsze spełnione (najniższym punktem jest (0, −1))
z dołączonym drugim warunkiem, co dostajemy dodatkowo to jedynie y≤1
9 sie 12:59
ite: Czy po połączeniu obu warunków
{<x,y>∊ℛxℛ | ∃z(y2+(x−z)2=1) ∨ ∃z((x−z)62+(y−z2)2=1)}
nie otrzymamy sumy obu figur
czyli pasa: x dowolne, −1≤y≤1 oraz zbioru punktów oddalonych od paraboli (z, z2) o co
najwyżej 1 ?
9 sie 23:24
ite: *(x−z)2
9 sie 23:25
Adamm:
no tak
czyli zbiór punktów (x, y) oddalonych od (z, z2) o co najwyżej 1, takich że y≤1
9 sie 23:29
ite:
Już ostatnie pytanie: czy warunek ∃z((x−z2)2+(y−z2)2=1) spełniałyby punkty (x, y)
oddalone od półprostej o początku w pkt(0,0) o co najwyżej 1?
9 sie 23:45
Adamm:
tak
10 sie 00:00
ite: Bardzo dziekuję za cierpliwość!
10 sie 00:02
Adamm:
To ja dziękuję, to było dosyć ciekawe zadanie.
10 sie 00:12